Дипломная

Исследовательские умения можно разделить на общие и специальные. К числу общих исследовательских умений, формирование и развитие которых происходит в процессе решения задач с параметрами, относятся: умение увидеть за данным уравнением с параметром различные классы уравнений, характеризующиеся общностью наличия количества и вида корней; умение владеть аналитическим и графоаналитическим методами....

Уравнения и неравенства с параметром как средство формирования исследовательских умений учащихся в 7-9 классах (реферат, курсовая, диплом, контрольная)

Дипломная работа

п о теме: Уравнения и неравенства с параметром как средство формирования исследовательских умений учащихся в 7 — 9 классах

Развитие творческих мыслительных способностей невозможно вне проблемных ситуаций, поэтому особое значение в обучении имеют нестандартные задачи. К ним относятся и задачи, содержащие параметр. Математическое содержание этих задач не выходит за пределы программы, тем не менее, их решение, как правило, вызывает у учащихся затруднения.

До реформы школьного математического образования в 60-х годах в школьной программе и учебниках были специальные разделы: исследование линейных и квадратных уравнений, исследование систем линейных уравнений. Где ставилась задача исследования уравнений, неравенств и систем в зависимости от каких-либо условий или параметров.

В настоящее время программа не содержит специальных упоминаний об исследованиях или параметрах в уравнениях или неравенствах. А ведь именно они и есть одно из эффективных средств математики, помогающих решить задачу формирования интеллектуальной личности, ставящуюся программой. Для устранения этого противоречия возникла необходимость создания элективного курса по теме «Уравнения и неравенства с параметрами». Именно этим и определяется актуальность данной работы.

Уравнения и неравенства с параметрами — прекрасный материал для настоящей исследовательской работы, но школьной программой задачи с параметрами не предусмотрены как отдельная тема.

Решение большей части задач школьного курса математики направлено на формирование у школьников таких качеств как владение правилами и алгоритмами действий в соответствии с действующими программами, умение проводить элементарные исследования.

Под исследованием в науке понимается изучение какого-либо объекта с целью выявления закономерностей его возникновения, развития, преобразования. В процессе исследования применяется накопленный опыт, имеющиеся знания, а так же методы и способы изучения объектов. Итогом исследования должно стать получение новых знаний. В процессе учебного исследования синтезируются накопленные учеником знания и опыт в изучении математических объектов.

В применении к параметрическим уравнениям и неравенствам можно выделить следующие исследовательские умения:

1) Умение выражать через параметр условия принадлежности данного параметрического уравнения к тому или иному классу уравнений;

2) Умение определять вид уравнения и указывать вид коэффициентов в зависимости от параметров;

3) Умение выражать через параметры, условия наличия решений параметрического уравнения;

4) В случае наличия корней (решений) уметь выражать условия наличия того или иного количества корней (решений);

5) Умение выражать через параметры сами корни параметрические уравнения (решения неравенства).

Развивающий характер уравнений и неравенств с параметрами определяется их способностью реализовывать многие виды мыслительной деятельности учащихся:

Выработка определенных алгоритмов мышления, Умение определить наличие и количество корней (в уравнении, системе);

Решение семейств уравнений, являющихся следствием данного;

Выражение одной переменной через другую;

Нахождение области определения уравнения;

Повторение большого объема формул при решении;

Знание соответствующих методов решения;

Широкое применение словесной и графической аргументации;

Развитие графической культуры учащихся;

Все вышесказанное позволяет говорить о необходимости изучения уравнений и неравенств с параметрами в школьном курсе математики.

В настоящее время класс задач с параметрами пока четко методически не отработан. Актуальность выбора темы элективного курса «Квадратные уравнения и неравенства с параметром» определяется значимостью темы «Квадратный трехчлен и его свойства» в школьном курсе математики и, вместе с тем, нехваткой времени на рассмотрение задач, связанных с исследованием квадратного трехчлена, содержащего параметр.

В своей работе мы хотим показать, что задачи с параметра не должны быть трудным дополнением к основному изучаемому материалу, которым могут овладеть только способные дети, а могут и должны использоваться в общеобразовательной школе, что обогатит обучение новыми методами и идеями, поможет учащимся развивать мышление.

Цель работы заключается в изучении места уравнений и неравенств с параметрами в курсе алгебры 7−9 классов, разработке элективного курса «Квадратные уравнения и неравенства с параметром» и методических рекомендаций по его проведению.

Объект исследования — процесс обучения математике в 7−9 классах общеобразовательной школы.

Предмет исследования — содержание, формы, методы и средства решения уравнений и неравенств с параметрами в средней общеобразовательной школе, обеспечение разработки элективного курса «Квадратные уравнения и неравенства с параметром».

Гипотеза исследования заключается в том, что данный элективный курс поможет обеспечить более углубленное изучение содержательной линии раздела математики «Уравнения и неравенства с параметрами», устранить расхождения в требованиях по математике, предъявленных к подготовке выпускников в школе и абитуриентов в вузе, расширить возможности развития мыслительной деятельности учащихся, если в процессе его изучения будут использованы:

· рассмотрение графических приемов решения квадратных уравнений и неравенств с параметром с помощью работы школьников с учебной литературой;

· решение задач на исследование квадратного трехчлена, содержащего параметр, с использованием самоконтроля школьников и взаимоконтроля;

· таблицы для обобщения материала по темам «Знак корней квадратного трехчлена», «расположение параболы относительно оси абсцисс»;

· использование разнообразных способов оценивания результатов обучения и накопительной системы баллов;

· изучение всех тем курса с предоставлением ученику возможности самостоятельно находить путь решения задачи.

В соответствии с целью, объектом, предметом и гипотезой исследования выдвигаются следующие задачи исследования:

· рассмотреть общие положения по изучению уравнений и неравенств с параметрами в 7−9 классах;

· разработать элективный курс по алгебре «Квадратные уравнения и неравенства с параметром» и методику его проведения.

В ходе исследования были использованы следующие методы:

· анализ литературы;

· анализ опыта разработки элективных курсов.

Глава 1. Психолого-педагогические особенности изучения темы « Уравнения и неравенства с параметрами» в курсе алгебры 7−9 класса

§ 1. Возрастные, физиологические и психологические осо бенности школьников 7−9 классов

Средний школьный возраст (подростковый) характеризуется бурным ростом и развитием всего организма. Наблюдается интенсивный рост тела в длину (у мальчиков за год наблюдается прирост на 6 — 10 сантиметров, а у девочек до 6 — 8 сантиметров). Продолжается окостенение скелета, кости приобретают упругость и твердость, возрастает сила мышц. Однако развитие внутренних органов происходит неравномерно, рост кровеносных сосудов отстает от роста сердца, что может вызвать нарушение ритма его деятельности, учащению сердцебиения. Развивается легочный аппарат, дыхание в этом возрасте учащенное. Объем мозга приближается к объему мозга взрослого человека. Улучшается контроль коры головного мозга над инстинктами и эмоциями. Однако процессы возбуждения все еще преобладают над процессами торможения. Начинается усиленная деятельность ассоциативных волокон.

В данном возрасте происходит половое созревание. Усиливается деятельность желез внутренней секреции, в частности половых желез. Появляются вторичные половые признаки. Организм подростка обнаруживает большую утомляемость, обусловленную кардинальными переменами в нем. Восприятие подростка более целенаправленно, организованно и планомерно, чем у младшего школьника. Определяющее значение имеет отношение подростка к наблюдаемому объекту. Внимание произвольно, избирательно. Подросток может долго сосредотачиваться на интересном материале. Запоминание понятий, непосредственно связанное с осмысливанием, анализом и систематизацией информации, выдвигается на первый план. Для подросткового возраста характерна критичность мышления. Для учащихся данного возраста свойственна большая требовательность к сообщаемой информации. Улучшается способность к абстрактному мышлению. Проявление эмоций у подростков часто бывает достаточно бурное. Особенно сильно проявляется гнев. Для данного возраста достаточно характерны упрямство, эгоизм, уход в себя, острота переживаний, конфликты с окружающими. Данные проявления позволили педагогам и психологам говорить о кризисе подросткового возраста. Формирование идентичности требует от человека переосмысления своих связей с окружающими, своего места среди других людей. В подростковом возрасте происходит интенсивное нравственное и социальное формирование личности. Идет процесс формирования нравственных идеалов и моральных убеждений. Часто они имеют неустойчивый, противоречивый характер.

Общение подростков с взрослыми существенно отличается от общения младших школьников. Подростки зачастую не рассматривают взрослых как возможных партнеров по свободному общению, они воспринимают взрослых как источник организации и обеспечения их жизни, причем организаторская функция взрослых воспринимается подростками чаще всего лишь как ограничительно — регулирующая.

Сокращается количество вопросов, обращенных к учителям. Задаваемые вопросы касаются, в первую очередь, организации и содержания жизнедеятельности подростков в тех случаях, в которых они не могут обойтись без соответствующих сведений и инструкций взрослых. Уменьшается число вопросов этического характера. По сравнению с предыдущим возрастом авторитет педагога как носителя социальных норм и возможного помощника в решении сложных жизненных проблем существенно снижается.

§ 2. Возрастные особенности учебной деят

Учение для подростка является главным видом деятельности. В учебной деятельности подростка имеются свои трудности и противоречия, но есть и свои преимущества, на которые может и должен опираться педагог. Большим достоинством подростка является его готовность ко всем видам учебной деятельности, которые делают его взрослым в собственных глазах. Его привлекают самостоятельные формы организации занятий на уроке, сложный учебный материал, возможность самому строить свою познавательную деятельность за пределами школы. Однако подросток эту готовность не умеет реализовать, так как он не владеет способами выполнения новых форм учебной деятельности.

Подросток эмоционально реагирует на новый учебный предмет, а у некоторых эта реакция исчезает довольно быстро. Нередко у них снижается и общий интерес к учению, к школе. Как показывает психологические исследования, основная причина заключена в несформированности у учащихся навыков учебной деятельности, что не дает возможности удовлетворить актуальную потребность возраста — потребность в самоутверждении.

Одним из способов повышения эффективности обучения является целенаправленное формирование мотивов учения. Это непосредственно связано с удовлетворением преобладающих потребностей возраста. Одна из таких потребностей — познавательная. При ее удовлетворении у него формируется устойчивые познавательные интересы, которые определяют его положительное отношение к учебным предметам. Подростков очень привлекает возможность расширить, обогатить свои знания, проникнуть в сущность изучаемых явлений, установить причинно-следственные связи. Они испытывают большое эмоциональное удовлетворение от исследовательской деятельности. Неудовлетворение познавательной потребности и познавательных интересов вызывает не только состояние скуки, безразличия, но порой и резко отрицательное отношение к «неинтересным предметам». При этом в равной степени имеет значение как содержание, так и процесс, способы, приемы овладения знаниями.

Интересы подростков различаются по направленности их познавательной деятельности. Одни учащиеся предпочитают описательный материал, их привлекают отдельные факты, другие стремятся разобраться в сущности изучаемых явлений, объяснить их с точки зрения теории, третьи проявляют большую активность при использовании знаний в практической деятельности, другие — к творческой, исследовательской деятельности. 15]

Наряду с познавательными интересами существенное значение при положительном отношении подростков к учению имеет понимание значимости знаний. Для них очень важно осознать, осмыслить жизненное значение знаний и, прежде всего, их значение для развития личности. Многие учебные предметы нравятся подростку потому, что они отвечают его потребностям всесторонне развитого человека. Убеждения и интересы, сливаясь воедино, создают у подростков повышенный эмоциональный тонус и определяют их активное отношение к учению.

Если же подросток не видит жизненного значения знаний, то у него могут сформировать негативные убеждения и отрицательное отношение к существующим учебным предметам. Существенно значение при отрицательном отношении подростков к учению имеет осознание и переживание ими неуспеха в овладении теми или иными учебными предметами. Страх перед неуспехом, боязнь поражения порой приводит подростков к поиску благовидных причин, чтобы не пойти в школу или уйти с урока. Эмоциональное благополучие подростка во многом зависит от оценки его учебной деятельности взрослыми. Нередко смысл оценки для подростка выступает в стремлении добиться успеха в учебном процессе и тем самым получить уверенность в своих способностях и возможностях. Это связано с такой доминирующей потребностью возраста, как потребность осознать, оценить себя как личность, свои сильные и слабые стороны. Как показывают исследования, именно в подростковом возрасте доминирующую роль играет самооценка. Для эмоционального благополучия подростка очень важно, чтобы оценка и самооценка совпадали. В противном случае возникает внутренний, а иногда и внешний конфликт.

В средних классах учащиеся приступают к изучению и освоению основ наук. Учащимися предстоит овладеть большим объемом знаний. Материал, подлежащий усвоению, с одной стороны требует более высокого, чем раньше уровня учебно-познавательной и мыслительной деятельности, а с другой стороны направлен на их развитие. Учащиеся должны овладеть системой научных понятий и терминов, поэтому новые учебные предметы предъявляют новые требования к способам усвоения знаний и направлены на развитие интеллекта высшего уровня — теоретического, формального, рефлексивного мышления. Такое мышление характерно для юношеского возраста, но начинает оно развиваться у младших подростков.

Новое в развитии мышления подростка заключается в его отношении к интеллектуальным задачам как к таким, которые требуют их предварительного мысленного решения. Умение оперировать гипотезами в решении интеллектуальных задач — важнейшее приобретение подростка в анализе действительности. Мышление предположениями является отличительным инструментом научного рассуждения, поэтому такое мышление называется рефлексивным. Хотя усвоение научных понятий в школе уже само по себе создаёт ряд объективных условий для формирования у школьников теоретического мышления, однако, оно формируется не у всех: у разных учащихся может быть разный уровень и качество его реальной сформированности.

Теоретическое мышление может формироваться не только при овладении школьными знаниями. Контролируемой и управляемой становится речь, причём в некоторых лично значимых ситуациях подростки особенно стремятся говорить красиво, правильно. В процессе и в результате усвоения научных понятий создаётся новое содержание мышления, новые формы интеллектуальной деятельности. Существенным показателем неполноценного усвоения теоретических знаний является неумение подростка решать задачи, требующие использования этих знаний.

Центральное место начинает занимать анализ содержания материала, его своеобразия и внутренней логики. Для одних подростков характерна гибкость в выборе путей заучивания, другие предпочитают какой-либо один способ, а некоторые стараются упорядочить и логически обработать любой материал. Умение логически обрабатывать материал часто развивается у подростков стихийно. От этого зависит не только успеваемость, глубина и прочность знаний, но и возможность дальнейшего развития интеллекта и способностей подростка.

§ 3. Организация учебной деят ельности школьников 7−9 классов

Организация учебной деятельности подростков — важнейшая и сложнейшая задача. Ученик среднего школьного возраста вполне способен понять аргументацию педагога, родителя, согласиться с разумными доводами. Однако в виду особенностей мышления, характерных для данного возраста, подростка уже не удовлетворит процесс сообщения сведений в готовом, законченном виде. Ему захочется проверить их достоверность, убедиться в правильности суждений. Споры с учителями, родителями, приятелями — характерная черта данного возраста. Их важная роль заключается в том, что они позволяют обменяться мнениями по теме, проверить истинность своих воззрений и общепринятых взглядов, проявить себя. В частности, в обучении большой эффект дает внедрение проблемных задач. Основы данного подхода в обучении были разработаны еще в 60 — 70 — е годы XX века отечественными педагогами. В основе всех действий при проблемном подходе лежит осознание отсутствия знаний для решения конкретных задач, разрешение противоречий. В современных условиях данный подход должен реализовываться в контексте уровня достижений современной науки, задач социализации учащихся.

Важно поощрять самостоятельность мышления, высказывание школьником собственной точки зрения, умение сравнивать, находить общие и отличительные черты, выделять главное, устанавливать причинно — следственные связи, делать выводы.

Для подростка большое значение будет иметь информация интересная, увлекательная, которая стимулирует его воображение, заставляет задуматься. Хороший эффект дает периодическая смена видов деятельности — не только на уроке, но и при подготовке домашних заданий. Разнообразие видов работы способно стать весьма результативным средством повышения внимания и важным способом предотвращения общей физической утомляемости, связанной, как и с учебной нагрузкой, так и с общим процессом кардинальной перестройки организма в период полового созревания. 20]

Учащиеся до изучения соответствующих разделов школьной программы часто уже располагают определенными житейскими представлениями и понятиями, которые позволяют им достаточно хорошо ориентироваться в повседневной практике. Это обстоятельство в тех случаях, когда их внимание специально не обращено на связь получаемых знаний с практической жизнью, лишает многих учащихся потребности в приобретении и усвоении новых знаний, так как последние не имеют для них практического смысла.

Нравственные идеалы и моральные убеждения подростков складываются под влиянием многочисленных факторов, в частности, усиления воспитательного потенциала обучения. В решении сложных жизненных проблем большее внимание следует уделять косвенным методам воздействия на сознание подростков: не преподносить готовую моральную истину, а подводить к ней, не высказывать категоричных суждений, которые подростки могут воспринять в «штыки».

§ 4. Учебное исследование в системе основных требований к содержанию математического образования и уровню подготовки учащихся

Уравнения и неравенства с параметрами — это прекрасный материал для настоящей исследовательской работы. Но школьной программой задачи с параметрами не предусмотрены как отдельная тема.

Проанализируем различные разделы учебного стандарта школ России с точки зрения выявления вопросов, связанных с обучением решению задач с параметрами.

Изучение программного материала дает возможность учащимся основной школы «получить начальные представления о задаче с параметрами, сводящийся к линейным и квадратным» и научиться строить графики функций, исследовать расположение этих графиков в координатной плоскости в зависимости от значений параметров, входящих в формулу.

В линии «функция» не упоминается слово «параметр», но говорится, что учащиеся имеют возможность «систематизировать и развить знания о функции; развить графическую культуру, научиться свободно „читать“ графики, отражать свойства функции на графике».

Проанализировав школьные учебники по алгебре таких коллективов авторов как: Алимов Ш. А. и др., Макарычев Ю. Н. и др., Мордкович А. Г. и др., приходим к выводу, что задачам с параметрами в данных учебных пособиях уделяется мало внимания. В учебниках для 7-х классов есть несколько примеров на исследование вопроса о числе корней линейного уравнения, на исследования зависимости расположения графика линейной функции у = kх и у = kх + b в зависимости от значений k. В учебниках для 8−9 классов в разделах типа «Задачи для внеклассной работы» или «Упражнения на повторение» дано по 2−3 задания на исследование корней в квадратных и биквадратных уравнениях с параметрами, расположения графика квадратичной функции в зависимости от значений параметров.

В программе по математике для школ и классов с углубленным изучением в объяснительной записке написано «раздел «Требования к математической подготовке учащихся» задает примерный объем знаний, умений и навыков, которым должны овладеть школьники. В этом объем, безусловно, входят те знания, умения и навыки, обязательное приобретение которых всеми учащимися предусмотрено требованиями программы общеобразовательной школы; однако предлагается иное, более высокой качество их сформированности. Учащиеся должны приобрести умения решать задачи более высокой по сравнению с обязательным уровнем сложности, точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач…"

Проанализируем некоторые учебные пособия для учащихся с углубленным изучением математики.

Формулировки таких задач и их решения, не выходят за рамки школьной программы, но сложности, с которыми сталкиваются учащиеся, объясняются, во-первых, наличием параметра, во-вторых, ветвлением решения и ответов. Однако, практика решения задач с параметрами полезна для развития и укрепления способности к самостоятельному логическому мышлению, для обогащения математической культуры.

В школе в общеобразовательных классах таким задачам уделяется, как правило, ничтожно мало внимания. Так как решение уравнений и неравенств с параметрами является, пожалуй, самым трудным разделом курса элементарной математики, то вряд ли целесообразно обучать решению таких задач с параметрами массового школьника, но сильных учащихся, проявляющих интерес, склонности и способности к математике, стремящихся действовать самостоятельно, учить решать такие задачи, безусловно, необходимо. Поэтому наряду с такими традиционными содержательно-методическими линиями школьного курса математики, как функциональная, числовая, геометрическая, линия уравнений и линия тождественных преобразований, должна занять определенное положение и линия параметров. Содержание материала и требования к учащимся по теме «задачи с параметрами» должны определяться, конечно, уровнем математической подготовки всего класса в целом и каждого в отдельности.

Учитель должен способствовать удовлетворению потребностей и запросов школьников, проявляющих интерес, склонности и способности к предмету. По интересующим учащихся вопросам можно организовать консультации, кружки, дополнительные занятия и факультативы. В полной мере это относится и к вопросу о задачах с параметрами.

§ 5. Учебное исследование в структуре познавательной деятельности школьников

В настоящий момент особенно остро встает вопрос подготовки ученика, стремящегося действовать самостоятельно, за рамками требований учителя, не ограничивающего сферу своих интересов и активного исследования предлагаемым ему учебным материалом, умеющего представлять и аргументировано отстаивать свое решение той или иной проблемы, умеющего конкретизировать или, наоборот, обобщать рассматриваемый результат, выявлять причинно-следственные связи и т. п. В связи с этим большое значение приобретают исследования, в которых анализируются основы психологии математического творчества детей школьного возраста, рассматривается проблема управления процессом мыслительной деятельности учеников, формирование и развитие у них умений самостоятельно приобретать знания, применять знания, пополнять и систематизировать их, проблема повышения активности познавательной деятельности школьников (Л.С. Выготский, П. Я. Крутецкий, Н. А. Менчинская, С. Л. Рубинштейн, Л.M. Фридман и др).

К исследовательскому методу обучения можно отнести два исследовательских метода: учебное и научное.

Решение существенной части задач школьного курса математики предполагает сформированными у учеников такие качества, как владение правилами и алгоритмами действий в соответствии с действующими программами, умение проводить элементарные исследования. Под исследованием в науке понимается изучение какого-либо объекта с целью выявления закономерностей его возникновения, развития преобразования. В процессе исследования применяется накопленный предшествующий опыт, имеющиеся знания, а также методы и способы (приемы) изучения объектов. Итогом исследований должно стать получение новых научных знаний.

В применении к процессу обучения математике в средней школе важно отметить следующее: к основным компонентам учебного исследования относят постановку проблемы исследования, осознание его целей, предварительный анализ имеющейся информации по рассматриваемому вопросу, условия и методы решения задач, близких к проблеме исследования, выдвижение и формулировка исходной гипотезы, анализ и обобщение полученных в ходе исследования результатов, проверка исходной гипотезы на основе полученных фактов, окончательная формулировка новых результатов, закономерностей, свойств, определение места найденного решения поставленной проблемы в системе имеющихся знаний. Основное место среди объектов учебного исследования занимают те понятия и отношения школьного курса математики, в процессе изучения которых выявляются закономерности их изменения и преобразования, условий их осуществления, единственности и т. п.

Серьезным потенциалом в формировании таких исследовательских умений, как умение целенаправленно наблюдать, сравнивать, выдвигать, доказывать или опровергать гипотезу, умение обобщать и др., обладают задачи на построение в курсе геометрии, уравнения и неравенства с параметрами в курсе алгебры, так называемые динамические задачи, в процессе решения которых учащиеся осваивают основные приемы мыслительной деятельности: анализ, синтез (анализ через синтез, синтез через анализ), обобщение, конкретизация и др., целенаправленно наблюдает изменяющиеся объекты, выдвигает и формулирует гипотезу относительно свойств рассматриваемых объектов, проверяет выдвинутую гипотезу, определяет место подученного результата в системе полученных ранее знаний, его практическую значимость. Решающее значение имеет организация учебного исследования учителем. Обучение приемам мыслительной деятельности, умение осуществлять элементы исследования — эти цели постоянно привлекают внимания учителя, побуждая его находить ответы на многие методические вопросы, связанные с решением рассматриваемой проблемы.

Изучение многих вопросов программы предоставляет прекрасные возможности для создания более цельной и полной картины, связанной с рассмотрением той или иной задачи.

В процессе учебного исследования синтезируются накопленные учеником знания, опыт в изучении математических объектов. Решающее значение в организации учебного исследования школьника имеет привлечение его внимания (сначала непроизвольного, а затем и произвольного), создание условий для наблюдения: обеспечение глубокого осознания, необходимого отношения ученика к работе, объекту изучения ("https://сайт", 9).

В школьном обучении математике имеют место тесно связанные между собой два уровня учебного исследования: эмпирический и теоретический. Первый характеризуется наблюдением за отдельными фактами, их классификации, установлению проверяемой на опыте закономерной связи между ними. Теоретический уровень учебного исследования отличается тем, что в результате ученик формулирует общие математические закономерности, на основе которых более глубоко интерпретируются не только новые факты, но и полученные на эмпирическом уровне.

Проведение учебного исследования требует от ученика применения как частных методов, характерных только для математики, так и общих; анализ, синтез, индукция, дедукция и др., применяемых при изучении объектов и явлений различных школьных дисциплин.

Решающее значение имеет организация учебного исследования учителем. В применении к процессу обучения математике в средней школе важно отметить следующее: к основным компонентам учебного исследования мы относим постановку проблемы исследования, осознание его целей, предварительный анализ имеющейся информации по рассматриваемому вопросу, условия и методы решения задач, близких к проблеме исследования, выдвижение и формулировка исходной гипотезы, анализ и обобщение полученных в ходе исследования результатов, проверка исходной гипотезы на основе полученных фактов, окончательная формулировка новых результатов, закономерностей, свойств, определение места найденного решения поставленной проблемы в системе имеющихся знаний. Основное место среди объектов учебного исследования занимают те понятия и отношения школьного курса математики, в процессе изучения которых выявляются закономерности их изменения и преобразования, условия их осуществления, единственности и т. п.

Подходящим для проведения учебного исследования является материал, относящийся к исследованию изучаемых в курсе алгебры функций. В качестве примера рассмотрим линейную функцию.

Задание: Исследуйте линейную функцию на четность и нечетность. Указание: рассмотрите случаи:

2) a = 0 и b? 0;

3) a? 0 и b = 0;

4) a? 0 и b? 0.

В результате исследования заполните таблицу, указав на пересечении соответствующей строки и столбца полученный результат.

В результате решения школьники должны получить следующую таблицу:

	четная и нечетная
	нечетная	ни четная, ни нечетная

Ее симметричность вызывает чувство удовлетворения, уверенности в правильности заполнения.

Формирование приемов мыслительной деятельности играет существенную роль как в общем развитии школьников, так и в целях привития им навыков проведения учебного исследования (в целом или фрагментарно).

Итогом учебного исследования служат субъективно новые знания о свойствах рассматриваемого объекта (отношения), об их практических приложениях. Эти свойства могут быть включены в программу по математике для средней школы, а могут и не входить в нее. Важно отметить, что новизна результата деятельности школьника определяется как характером поиска способа осуществления деятельности, самим способом деятельности, так и местом полученного результата в системе знаний того ученика.

Метод обучения математике с использованием учебного исследования носит название исследовательского, независимо от того, реализуется ли схема учебного исследования в полном объеме или фрагментарно.

При реализации каждого этапа учебного исследования обязательно присутствуют элементы как исполнительской, так и творческой деятельности. Наиболее четко это наблюдается в случае самостоятельного проведения учеником того или иного исследования. Также при учебном исследовании одни этапы могут быть реализованы учителем, другие — самим учеником. Уровень самостоятельности зависит от многих факторов, в частности, от уровня сформированности, умения наблюдать тот или иной объект (процесс), от умения сосредоточить свое внимание на одном и том же предмете иногда в течение довольно длительного времени, умения увидеть проблему, четко и недвусмысленно ее сформулировать, умения находить и использовать подходящие (порой неожиданные) ассоциации, умения сосредоточенно анализировать имеющиеся знания с целью отбора нужной информации и т. п.

Также невозможно переоценить влияние воображения, интуиции, вдохновения, способности (а может быть и талантливости или гениальности) ученика на успешность его исследовательской деятельности.

§ 6 . Исследование в системе методов обучения

Методам обучения, от которых зависит немалый успех работы учителя и школы в целом, посвящен не один десяток фундаментальных исследований. И, несмотря на это проблема методов обучения, как в теории обучения, так и в педагогической практике остается весьма актуальной. Понятие метода обучения является весьма сложным. Это обуславливается исключительной сложностью того процесса, который призвана отражать эта категория. Многие авторы считают метод обучения способом организации учебно-познавательной деятельности учащихся.

Слово «метод» греческого происхождения и в переводе на русский язык означает исследование, способ. «Метод — в самом общем значении — способ достижения цели, определенным образом упорядоченная деятельность» . Очевидно, что в процессе обучения метод выступает как связь деятельности учителя и учащихся по достижению определенных учебно-воспитательных целей. С этой точки зрения каждый метод обучения органически включает в себя обучающую работу учителя (изложение, объяснение изучаемого материала) и организацию активной учебно-познавательной деятельности учащихся. Таким образом, понятие метода обучения отражает:

1 .Способы обучающей работы учителя и способы учебной работы учащихся в их взаимосвязи.

2. Специфику их работы по достижению различных целей обучения. Таким образом, методы обучения — это способы совместной деятельности учителя и учащихся, направленные на решение задач обучения, то есть дидактических задач.

То есть под методами обучения следует понимать способы обучающей работы учителя и организации учебно-познавательной деятельности учащихся по решению различных дидактических задач, направленных на овладение изучаемым материалом. Одной из острых проблем современной дидактики является проблема классификации методов обучения. В настоящее время нет единой точки зрения по этому вопросу. В связи с тем, что разные авторы в основу подразделения методов обучения на группы и подгруппы кладут разные признаки, существует ряд классификаций. Но в 20-е годы в советской педагогике велась борьба против методов схоластического обучения и механической зубрежки, процветавших в старой школе и предпринимались поиски таких метод, которые обеспечивали бы сознательное, активное и творческое овладение знаниями учащимися. Именно в те годы педагог Б. В. Виевятский развивал положение о том, что в обучении может быть только два метода: метод исследовательский и метод готовых знаний. Метод готовых знаний, естественно, подвергался критике. В качестве важнейшего метода обучения и раньше и сейчас признавался исследовательский метод, суть которого сводилась к тому, что учащиеся якобы все должны познавать на основе наблюдения и анализа изучаемых явлений, самостоятельно подходя к необходимым выводам. Тот же исследовательский метод на занятиях может применяться далеко не по всем темам.

Так же суть этого метода состоит в том, что учитель расчленяет проблемную задачу на подпроблемы, а учащиеся осуществляют отдельные шаги поиска ее решения. Каждый шаг предполагает творческую деятельность, но целостное решение проблемы пока отсутствует. При исследовании учащиеся овладевают методами научного познания, формируется опыт исследовательской деятельности. Деятельность учащихся, обучаемых с использованием этого метода, заключается в освоении ими приемов самостоятельной постановки проблем, нахождения способов их решения, исследовательские задания, постановки и разработки проблем, которые предъявляют им учителя.

Можно также отметить, что психология устанавливает некоторые закономерности с возрастной психологией. Прежде, чем с учащимися начинать работу с использованием методов, надо хорошо изучить методы исследования его возрастной психологии. Знакомство с этими методами может оказать практическую пользу непосредственно организаторам этого процесса, так как эти методы пригодны не только для собственного научного исследования, но и для организации углубленного изучения детей в практических учебно-воспитательных целях. Индивидуальный подход в обучении и воспитании предполагаем хорошее знание и понимание индивидуально-психологических особенностей учащихся, своеобразия их личности. Следовательно, учителю необходимо овладеть умением изучать учащихся, видеть не серую, однородную ученическую массу, а коллектив, в котором каждый представляет собой нечто особое, индивидуальное, своеобразное. Такое изучение входит в задачу каждого учителя, но его нужно еще правильно организовать.

Один из основных методов организации — метод наблюдения. Разумеется, психику непосредственно наблюдать нельзя. Этот метод предполагает опосредованное познание индивидуальных особенностей психики человека через изучение его поведения. То есть, здесь нужно судить учащегося по индивидуальным особенностям (действиям, поступкам, речи, внешнему облику и т. д.), психическому состоянию учащегося (процессам восприятия, памяти, мышления, воображения и т. д.), и по чертам его личности, темперамента, характера. Все это необходимо для учащегося, с которым работает учитель с применением исследовательского метода обучения при выполнении каких-то заданий.

Решение существенной части задач школьного курса математики предполагает сформированными у учеников такие качества как владение правилами и алгоритмами действий в соответствии с действующими программами, умение проводить элементарное исследование. Под исследованием в науке понимается изучение какого-либо объекта для выявления закономерностей его возникновения, развития, преобразования. В процессе исследования применяется накопленный предшествующий опыт, имеющиеся знания, а также методы и способы (приемы) изучения объектов. Итогом исследования должно стать получение новых научных знаний. Обучение приемам мыслительной деятельности, умение осуществлять элементы исследования — эти цели постоянно привлекают внимание учителя, побуждая его находить ответы на многие методические вопросы, связанные с решением рассматриваемой проблемы. Изучение многих вопросов программы предоставляет прекрасные возможности для создания более цельной и полной картины, связанной рассмотрением той или иной задачи. Исследовательский метод обучения математике естественно вписывается в классификацию метод обучения в зависимости от характера деятельности школьников, степени их познавательной самостоятельности. Для успешной организации исследовательской деятельности школьника учитель должен понимать и учитывать как его личностные качества, так и процессуальные особенности этого вида деятельности, а также уровень владения школьником изученным материалом курса. Невозможно переоценить влияние воображения, интуиции, вдохновения, способности ученика на успешность его исследовательской деятельности.

Формы заданий при исследовательском методе могут быть различны. Это могут быть задания, поддающиеся быстрому решению в классе и дома или задания, требующие целого урока. Большинство исследовательских заданий должны представлять собой небольшие поисковые задания, требующие прохождения всех или большинства этапов процесса исследования. Целостное их решение обеспечит выполнение исследовательским методом его функций. Этапами процесса исследования являются следующие:

1 Целенаправленное наблюдение и сравнение фактов и явлений.

Выявление непонятных явлений, подлежащих исследованию.

Предварительный анализ имеющейся информации по рассматриваемому вопросу.

4. Выдвижение и формулировка гипотезы.

5. Построение плана исследования.

Осуществление плана, выяснения связей изучаемого явления с другими.

Формулирование новых результатов, закономерностей, свойств, определение места найденного решения поставленных исследований в системе имеющихся знаний.

Проверка найденного решения.

Практические выводы о возможном применении новых знаний.

§ 7 . Умение исследовать в сист еме специальных знаний

Умение — это сознательное применение имеющихся у ученика знаний и навыков для выполнения сложных действий в различных условиях, т. е. для решения соответствующих задач, ибо выполнение каждого сложного действия выступает для ученика как решение задачи.

Исследовательские умения можно разделить на общие и специальные. К числу общих исследовательских умений, формирование и развитие которых происходит в процессе решения задач с параметрами, относятся: умение увидеть за данным уравнением с параметром различные классы уравнений, характеризующиеся общностью наличия количества и вида корней; умение владеть аналитическим и графоаналитическим методами.

К числу специальных исследовательских умений можно отнести умения, формирование и развитие которых происходит в процессе решения конкретного класса задач.

При решении линейных уравнений, содержащих параметр, формируются следующие специальные умения:

§ Умение выявлять особые значения параметра, при которых данное линейное уравнение имеет:

Единственный корень;

Бесконечное множество корней;

3) Не имеет корней;

Умение интерпретировать ответ на языке исходного задания. К числу специальных исследовательских умений, формирование и развитие которых происходит в процессе решения линейных неравенств, содержащих параметр относятся:

§ Умение увидеть коэффициент при неизвестном и свободный член как функцию параметра;

§ Умение выявлять особые значения параметра, при которых данное линейное неравенство имеет в качестве решения:

1) Промежуток;

2) Не имеет решений;

§ Умение интерпретировать ответ на языке исходного задания К числу специальных исследовательских умений, формирование и развитие которых происходит в процессе решения квадратных уравнений, содержащих параметр, относятся:

§ Умение выявлять особое значение параметра, при котором старший коэффициент обращается в ноль, т. е. уравнение становиться линейным и находить решение полученного уравнения при выявленных особых значениях параметра;

§ Умение решать вопрос о наличии и количестве корней данного квадратного уравнения в зависимости от знака дискриминанта;

§ Умение выражать через параметр корни квадратного уравнения (в случае их наличия);

К числу специальных исследовательских умений, формирование и развитие которых происходит в процессе решения дробно-рациональных уравнений, содержащих параметр, сводящихся к квадратным, относятся:

§ Умение приводить дробно-рациональное уравнение, содержащее параметр, к квадратному уравнению, содержащему параметр.

К числу специальных исследовательских умений, формирование и развитие которых происходит в процессе решения квадратных неравенств, содержащих параметр относятся:

§ Умение выявлять особое значение параметра, при котором старший коэффициент обращается в ноль, т. е неравенство становится линейным и находить множество решений полученного неравенства при особых значениях параметра;

§ Умение выражать через параметр множество решений квадратного неравенства.

Ниже перечислены учебные умения, переходящие в учебно-исследовательские, а также исследовательские умения.

6−7 класс:

— оперативно использовать старые знания в ситуации приобретения новых;

— переносить свободно комплекс умственных действий с одного материала на другой, с одного предмета на другой;

распространять полученные знания на большую совокупность объектов;

сочетать процесс «свертывания» и «развертывания» знаний;

целенаправленно обобщать идеи текста с помощью выделения главных мыслей в его отрезках, частях;

систематизировать и классифицировать информацию;

— сопоставлять информацию по системам признаков с выделением черт сходства и различия;

— уметь связать символический язык с письменной и устной речью;

— анализировать и планировать методы предстоящей работы;

«сцеплять» быстро, свободно компоненты новых знаний;

уметь лаконично излагать основные мысли, факты текста;

— получать новые знания путем движения от системообразующих знаний к конкретному с помощью схем, таблиц, конспектов и т. д. ;

использовать различные формы записей в процессе длительного слушания;

выбирать оптимальные пути решения;

доказывать или опровергать с помощью взаимосвязанных приемов;

— пользоваться различными видами анализа и синтеза;

— рассматривать проблему с разных точек зрения;

— высказывать суждение в виде алгоритма мыслей.

Математическому образованию в процессах формирования мышления или умственного развития учащихся должно отводиться и отводится особое место, потому что средства обучения математике наиболее эффективно воздействуют на многие основные компоненты целостной личности и прежде всего на мышление.

Таким образом, уделяется особое внимание развитию мышления учащегося, так как именно оно связано со всеми другими мыслительными функциями: воображением, гибкостью ума, широтой и глубиной мысли и т. д. Отметим что, рассматривая развитие мышления в контексте личностно-ориентированного обучения, следует помнить, что необходимым условием для реализации такого развития является индивидуализация обучения. Именно оно обеспечивает учет особенностей мыслительной деятельности учащихся различных категорий.

Путь к творчеству индивидуален. Вместе с тем, все учащиеся в процессе изучения математики должны ощутить ее творческий характер, познакомиться в процессе обучения математике с некоторыми умениями и навыками творческой деятельности, которые им будут нужны в их дальнейшей жизни и деятельности. Для решения этой сложной задачи преподавание математики должно быть построено так, чтобы ученик чаще искал новые комбинации, преобразовывая вещи, явления, процессы действительности, искал неизвестные связи между объектами.

Прекрасным способом приобщения учащихся к творческой деятельности при обучении математике является самостоятельная работа во всех ее видах и проявлениях. Весьма принципиальным в этом отношении является высказывание академика П. Л. Капицы о том, что самостоятельность является одним из самых основных качеств творческой личности, так как воспитание творческих способностей в человеке основывается на развитии самостоятельного мышления.

Уровень подготовленности учащихся и учебных групп к самостоятельной творческой деятельности можно определить, ответив на следующие вопросы:

Насколько эффективно школьники могут пользоваться конспектами, опорным конспектом, а также читать схемы и разные виды таблиц?

Умеют ли учащиеся объективно оценивать предложенные идеи при решении проблемной задачи учителем, учитывать возможность их применения? 3) Насколько школьники быстро переходят от одного способа решения проблемы к другому? 4) Проанализировать эффективность ориентирования учащихся в ходе урока на самоорганизацию самостоятельной работы; 5) Исследовать способность учащихся к моделированию и гибкому решению проблем.

Глава 2. Методологический анализ темы «Уравнения и неравенства с параметрами» и разработка элективного курса «Квадратные уравнения и неравенства с параметром»

§ 1. Роль и место параметрических уравнений и неравенств в формировании исследовательских умени й учащихся

Несмотря на то, что программа по математике средней общеобразовательной школы не упоминает в явном виде о задачах с параметрами, было бы ошибкой утверждать, что вопрос о решении задач с параметрами никоим образом не затрагивается в рамках школьного курса математики. Достаточно вспомнить школьные уравнения: ax2+bx+c=0, у=kх, у=kх+b, ax=b, в которых а, b, с, k не что иное, как параметры. Но в рамках школьного курса не заостряется внимание на таком понятии, параметр, в чем его отличие от неизвестного.

Опыт показывает, что задачи с параметрами являются наиболее сложным в логическом и техническом планах разделом элементарной математики, хотя с формальной точки зрения математическое содержание таких задач не выходит за пределы программ. Это вызвано различными точками зрения на параметр. С одной стороны, параметр можно рассматривать как переменную, которая при решении уравнений и неравенств считается постоянной величиной, с другой -- параметр — это величина, численное значение которой не задано, но должно считаться известным, причем параметр может принимать произвольные значения, т. е. параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойную природу. Во-первых, предполагаемая известность позволяет обращаться с параметром как с числом, а во-вторых, степень свободы ограничивается его неизвестностью.

В каждом из описаний природы параметров имеется неопределенность — на каких этапах решения параметр может рассматриваться в качестве константы и когда играет роль переменной величины. Все эти противоречивые характеристики параметра могут в самом начале знакомства вызвать у учащихся некий психологический барьер.

В связи с этим на начальном этапе знакомства с параметром очень полезно как можно чаще прибегать к наглядно-графической интерпретации полученных результатов. Это не только позволяет преодолеть естественную неуверенность учеников перед параметром, но и дает учителю возможность параллельно, в качестве пропедевтики, приучать учеников при решении задач использовать графические приемы доказательства. Не следует также забывать, что использование хотя бы схематических графических иллюстраций в некоторых случаях помогает определить направление исследований, а иногда и позволяет сразу подобрать ключ к решению задачи. Ведь для определенных типов задач даже примитивный рисунок, далекий от настоящего графика, дает возможность избежать различного рода ошибок и более простым способом получить ответ к уравнению или неравенству.

Решение математических задач вообще является наиболее трудной частью деятельности школьников при изучении математики и объясняется это тем, что для решения задач требуется достаточно высокий уровень развития интеллекта высшего уровня, т. е. теоретического, формального и рефлексивного мышления, а такое мышление, как уже отмечалось, еще только развивается в подростковом возрасте.

Урок по элективному курсу

по теме: «Решение уравнений и неравенств с параметрами»

(Урок обобщения и повторения)

Цель: 1.Повторить и обобщить знания учащихся методов решения уравнений и неравенств с параметрами; закрепить умения применять знания при решении конкретных заданий; 2. Развивать логическое мышление; 3.Воспитывать внимание и аккуратность.

План урок: I. Организационный момент_________________________2 мин.

II. Актуализация опорных знаний:

1. Повторение__________________________________3 мин.
2. Устная работа________________________________3 мин.
3. Работа по карточкам (во время 1 и 2)

III. Решение упражнений___________________________22 мин.

IY. Выполнение теста______________________________8 мин.

Y. Подведение итогов, постановка домашнего задания__2 мин.

Х о д у р о к а:

I. Организационный момент .

Учитель: - Здравствуйте, ребята. Приятно вас всех видеть, мы начинаем наш урок. Сегодня на уроке наша цель - повторить и отработать знания, умения и навыки, полученные на прошлых уроках при изучении данной темы.

II . Актуализация опорных знаний:

1) Повторение.

Учитель: - Итак, повторим.

Что называется линейным уравнением с параметрами?

Какие случаи мы рассматривали при решении таких уравнений?

Приведите примеры линейных уравнений с параметрами.

Приведите примеры линейных неравенств с параметрами.

2) Устная работа.

Задание: Приведите данное уравнение к линейному виду.

На доске:

а) 3а х – 1 =2 х ;

б) 2+5 х = 5а х ;

в) 2 х – 4 = а х + 1.

3) Работа по карточкам.

III . Решение упражнений.

Задание 1. Решить уравнение с параметром а.

3(ах + 1) + 1 = 2(а – х) + 1.

Задание выполняется на доске и в тетрадях.

Задание 2. При каком значении а, прямая у = 7ах + 9, проходит через

т. А(-3;2) ?

Задание выполняется самостоятельно у доски одним учеником. Остальные работают в тетрадях, затем сверяются с доской.

Физкульт. минутка.

Задание 3. При каком значении а, уравнение 3(ах – а) = х – 1 имеет

Бесконечно много решений?

Данное задание предлагается решить самостоятельно учащимся в тетрадях. Затем проверить ответы.

Задание 4. При каком значении параметра а , сумма корней уравнения

2х² + (4а² - 2)х – (а² + 1) = 0 равна 1?

Задание выполняется комментированием с места.

Задание 5. Решите неравенство с параметром р :

р(5х – 2)

Данное задание выполняется у доски и в тетрадях.

IY. Выполнение теста.

Учащимся выдаются индивидуальные листы с заданиями:

1) Является ли уравнение 6(ах + 1) + а = 3(а – х) + 7 линейным?

А) да; б) нет; в) можно привести к линейному

2) Уравнение (2ах + 1)а = 5а – 1 приведено к виду линейного уравнения

А) нет; б) да;

3) При каком значении параметра а прямая у = ах – 3 проходит через

Т. А(-2;9) ?

А) а = 1/6; б) а = 1/2; в) а = -6; г) а = 6.

4) При каком а уравнение 2ах + 1 = х имеет корень, равный -1?

а) а = -1; б) а = 0; в) а = 1; г) а = 1/2.

5) Если у квадратного уравнения ах² + вх + с = 0 Д ах² + вх + с >0 зависит от

А) значения в ; б) значения а ; в) значения -в/а ;

г) не имеет решений.

О т в е т ы к т е с т у: в; а; в; в; б.

YII. Подведение итогов урока. Постановка домашнего задания.

Учитель: - Сегодня на уроке мы повторили и закрепили знания, полученные на прошлых уроках, отработали необходимые умения при выполнении различных заданий. Я думаю, что вы поработали хорошо, молодцы.

Кроме поставленных за урок оценок, можно оценить работу на уроке еще ряда учащихся.

Учитель : - Запишите домашнее задание:

На доске:

Решить неравенство: х² - 2ах + 4 > 0.

Урок окончен.

ФБГОУ ВПО «Мордовский государственный

педагогический институт имени М.Е. евсевьева»

ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ

Кафедра математики и методики обучения математики

КУРСОВАЯ РАБОТА

Методика формирования умений решать уравнения и неравенства с параметрами в курсе основной общеобразовательной школе

студентка группы МДМ-110 А.И. Зимина

Специальность: 050201.65 «Математика» с дополнительной специальностью 050202 «Информатика»

Саранск 2014

Введение

Теоретические основы линий уравнений и неравенств в школьном курсе математики

1 Виды уравнений в школьном курсе математики

2 Виды неравенств в школьном курсе математики

3 Особенности решения уравнений с параметрами

4 Особенности решения неравенств с параметрами

Заключение

Список используемой литературы

Введение

На современном этапе развития школьного образования становятся приоритетными развивающие цели обучения. В связи с этим при изучении математики особую значимость приобретает организованное обучение приемам мышления, рационального выполнения учебной деятельности, что исключительно важно при усвоении трудных тем и решении сложных задач таких, как уравнения и неравенства с параметрами. Именно недостаточная сформированность приемов учебной деятельности является одной из причин того, что большинство учащихся совершает ошибки или испытывает затруднения при решении даже несложных задач такого рода.

Изучением задач с параметрами, их роли в обучении, понятий, связанных с их решением, в разные годы занимались М.И. Башмаков, Г.В. Дорофеев, М.И. Зайкин, Т.А. Иванова, Г.Л. Луканкин, Я.Л. Крейнин, В.К. Марков, А.Г. Мордкович, Н.Х. Розов, Г.И. Саранцев, Р.А. Утеева и др. Многие из них подчеркивали важность обучения школьников приемам решения уравнений и неравенств с параметрами прежде всего в связи с необходимостью подготовки учащихся к выполнению работ итоговой аттестации и различного рода конкурсных испытаний. При этом большинство авторов характеризует задачи с параметрами как исследовательские задачи, требующие высокой логической культуры и техники исследования; как наиболее сложные в логическом и семантическом плане вопросы элементарной математики. В этой связи В.В. Вересова, В.И. Горбачев, Н.С. Денисова, В.Н. Литвиненко, А.Г. Мордкович, Т.Н. Полякова, Г.А. Ястребинецкий и др. справедливо замечают, что для описания процесса их решения необходимо использовать систему понятий, математических утверждений и фактов, определяемую фундаментальными математическими идеями; некоторые из них предпринимают попытки к ее разработке. Однако в многочисленных пособиях и руководствах справочного и методического характера для поступающих в вузы рассматриваются лишь частные приемы решения конкретных уравнений и неравенств с параметрами, чаще всего в рамках широкого спектра конкурсных заданий.

Уравнения и неравенства, содержащие параметр, не изучаются систематически в школьном курсе математики, а рассматриваются лишь отдельные их простейшие примеры. Поэтому методы и приемы решения таких задач большинству учащихся не известны.

Актуальность данной темы состоит в том, что анализируя экзаменационные работы по математике, приходишь к выводу, что за курс математики в общеобразовательной школе учащимися должны быть отработаны умения решения задач с параметрами. Кроме непосредственной подготовки учащихся к экзаменам по данному разделу математики (решение задач с параметрами), главная его задача - поднять на более высокий уровень изучение математики в школе, следующий за развитием умений и навыков решения определенного набора стандартных задач.

Объект исследования: процесс формирования умений решать уравнений и неравенств с параметрами в школьном курсе метематике основной школы.

Предмет исследования: уравнения и неравенства с параметрами.

Цель исследования: выделить виды, методы решения уравнений и неравенств с параметрами в школьном курсе математике.

Для достижения поставленной цели необходимо было решить следующие задачи:

) Изучить и проанализировать специальную литературу по проблеме исследования;

)Рассмотреть роль уравнений и неравенств в школьном курсе математике;

1. Теоретические основы линий уравнений и неравенств в школьном курсе математики

Ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики организовано в содержательно-методическую линию уравнений и неравенств. Здесь рассматриваются вопросы формирования понятий уравнения и неравенства, общих и частных методов их решения, взаимосвязи изучения уравнений и неравенств с числовой, функциональной и другими линиями школьного курса математики.

Выделенным областям возникновения и функционирования понятия уравнения в алгебре соответствуют три основных направления развертывания линии уравнений и неравенств в школьном курсе математики.

а) Прикладная направленность линии уравнений и неравенств раскрывается главным образом при изучении алгебраического метода решения текстовых задач. Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.

В настоящее время ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, неравенств и их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.

б) Теоретико-математическая направленность линии уравнений и неравенств раскрывается в двух аспектах: во-первых, в изучении наиболее важных классов уравнений, неравенств и их систем и, во-вторых, в изучении обобщенных понятий и методов, относящихся к линии в целом. Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений и неравенств связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение линии в целом, поскольку они описывают то общее, что имеется в процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений и неравенств.

в) Для линии уравнений и неравенств характерна направленность на установление связей с остальным содержанием курса математики. Эта линия тесно связана с числовой линией. Основная идея, реализуемая в процессе установления взаимосвязи этих линий, - это идея последовательного расширения числовой системы. Все числовые области, рассматриваемые в школьной алгебре и началах анализа, за исключением области всех действительных чисел, возникают в связи с решением каких-либо уравнений, неравенств, систем. Например, числовые промежутки выделяются неравенствами или системами неравенств. Области иррациональных и логарифмических выражений связаны соответственно с уравнениями (k-натуральное число, большее 1.

Связь линии уравнений и неравенств с числовой линией двусторонняя. Приведенные примеры показывают влияние уравнений и неравенств на развертывание числовой системы. Обратное влияние проявляется в том, что каждая вновь введенная числовая область расширяет возможности составления и решения различных уравнений и неравенств.

Линия уравнений и неравенств тесно связана также и с функциональной линией. Одна из важнейших таких связей приложения методов, разрабатываемых в линии уравнений и неравенств, к исследованию функции (например, к заданиям на нахождение области определения некоторых функций, их корней, промежутков знакопостоянства и т.д.). С другой стороны, функциональная линия оказывает существенное влияние как на содержание линии уравнений и неравенств, так и на стиль ее изучения. В частности, функциональные представления служат основой привлечения графической наглядности к решению и исследованию уравнений, неравенств и их систем.

1 Виды уравнений в школьном курсе математике

Понятие «уравнение » относится к важнейшим общематематическим понятиям.

Существуют различные трактовки понятия «уравнение».

И.Я. Виленкин и др. приводит логико - математическое определение уравнения. Пусть на множестве М зафиксирован набор алгебраических операций, х - переменная на М; тогда уравнением на множестве М относительно x называется предикат вида, где и - термы относительно заданных операций, в запись которого входит символ.Аналогично определиться уравнение от двух и более переменных.

Принятые в логики термины «терм» и «предикат» соответствуют такие термины школьной математики как «выражение» и «предложение с переменной». Поэтому наиболее близко к приведенному формальному определению можно считать следующее определение: «Предложение с переменной, имеющий вид равенства между двумя выражениями с этой переменной, называется уравнением». Такое определение приведено в учебнике «Алгебра и начала анализа» А.Н Колмогоров и др. Равенство с переменной называется уравнением. Значение переменной при котором равенство с переменной обращается в верное числовое равенство, называется корнем уравнения.

Часто, особенно в начале систематического курса алгебры, понятие уравнение вводится по средством выделение его из алгебраического метода решения задач. Например, в учебнике Ш.А.Алимова и др. понятие уравнение вводиться на материале текстовой задачи. Переход к понятию уравнения осуществляется на основе анализа некоторых формальных особенностей записи, выражающих содержание данной задачи в алгебраической форме: «Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением». Указываемый способ введения понятия уравнения соответствует еще одному компоненту понятия уравнения - прикладному.

Еще один подход к понятию уравнения получается при составления области определения уравнения и множества его корней. Например, в учебнике Д.К.Фадеева «Буквенное равенство, которое не обязательно превращается в верное числовое равенство при допустимых наборов букв, называется уравнение».

Можно встретить и третий вариант определения, роль которого проявляется при изучения графического метода решения уравнений: «Уравнение - это равенство двух функций».

Среди всех изучаемых в курсе математике типов уравнений В.И. Мишин выделяет сравнительно ограничение количество основных типов. к их числу относится: линейное уравнение с одним неизвестным, систему двух линейных уравнений с двумя неизвестными, квадратные уравнения, простейшие иррациональные и трансцендентные.

Ю.М.Колягин и др. классифицируют по виду функций, представляющих правую и левую части уравнений:

Уравнение называется:

алгебраическим, если и - алгебраические функции;

трансцендентным, если хотя одним из функций и трансцендентная;

рациональным алгебраическим (или просто рациональным) , если алгебраические функции и рациональные;

иррациональным алгебраическим(или просто иррациональным), если хотя бы одна из алгебраических функций и иррациональная;

целым рациональным, если функция и целые рациональные;

дробным рациональным, если хотя бы одна из рациональных функций и дробная рациональная.

Уравнение, где - многочлен стандартного вида, называется линейным (первой степени), квадратным(во второй степени), кубическим (третьей степени) и вообще - ой степени, если многочлен, имеет соответственно первую, вторую, третью и вообще - ую степень.

В школе изучаются несколько типов уравнений. К их числу относятся: линейные уравнения с одной не известной, квадратные уравнения, иррациональные и трансцендентные уравнения, рациональные уравнения. Эти типы уравнений изучаются с большой тщательностью, для них указывается и доводиться до автоматизма выполнение алгоритма решения, указывается форма, в котором должен записываться ответ.

Виды уравнений и методы решения:

) Линейное уравнение

Уравнением с одной переменной, называется равенство, содержащее только одну переменную.

Корнем (или решением) уравнения называется такое значение переменной, при котором уравнение превращается в верное числовое равенство.

Найти все корни уравнения или доказать, что их нет - это значит решить уравнение.

Пример 1: Решить уравнение.

;

;

) Квадратное уравнение

Квадратное уравнение - это уравнение вида, где коэффициенты a, b и c - любые действительные числа, причем а≠0.

Корнями квадратного уравнения называют такие значения переменной, при которых квадратное уравнение обращается в верное числовое равенство.

Решить квадратное уравнение - значит найти все его корни или установить, что корней нет.

Пример 2: Решить уравнение

Данное уравнение можно решить либо через Теорему Виета, либо через дискриминант.

Ответ: х1=-1, х2=-2.

) Рациональные уравнения

рациональные уравнения - уравнения вида

где и многочлены, атак же уравнения вида, где и - рациональные.

Пример 3: Решить уравнение

) Иррациональные уравнения

Иррациональные уравнения - это уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.

Пример 4: Решить уравнение

Возведем обе части в квадрат:

) Показательные и логарифмические уравнения

При решения показательных уравнений используются два основных метода: а) переход от уравнения к уравнению;б) введения новых переменных. Иногда приходиться применять исскуственные приемы.

Логарифмические уравнения - решаются тремя методами, то есть переход от уравнения к уравнению - следствию;метод введения новых переменных логарифмирования, то есть переход от уравнения к уравнению.

А так же во многих случаях при решения логарифмического уравнения приходиться использовать свойства логарифма произведения, частного, степени, корня.

2 Виды неравенств в школьном курсе

В целом изучение неравенств в школьном курсе математики организовано так же, как и уравнений.

Отметим ряд особенностей изучения неравенств.

Как и в случае уравнений отсутствует теория равносильности неравенств. Учащимся предлагаются её незначительные фрагменты, приведённые в содержании учебного материала.

Большинство приёмов решения неравенств состоит в переходе от данного неравенства a>b к уравнению а=b и последующем переходе от найденных корней уравнения к множеству решений исходного неравенства. Например, такая ситуация возникает при решении рациональных неравенств методом интервалов, при решении простейших тригонометрических неравенств.

В изучении неравенств большую роль играют наглядно - графические средства.

Два выражения (числовые или буквенные), соединённые одним из знаков: «больше» (>), «меньше» (<), «больше или равно» (≥), «меньше или равно» (≤) образуют неравенство (числовое или буквенное). Любое справедливое неравенство называется тождественным.

В зависимости от знака неравенства мы имеем либо строгие неравенства (> , <), либо нестроги (≥ , ≤).

Буквенные величины, входящие в неравенство, могут быть как известными, так и неизвестными.

Решить неравенство - это найти границы, внутри которых должны находиться неизвестные, так чтобы неравенство было тождественным.

Основные свойства неравенств:

Если a < b, то b > a; или если a > b, то b < a .

Если a > b, то a + c > b + c; или если a < b, то a + c < b + c. То есть, можно прибавлять (вычитать) одно и то же число к обеим частям неравенства.

Если a > b и c > d, то a + c > b + d . То есть, неравенства одного смысла (с одинаковым знаком > или <) можно почленно складывать.

Если a > b и c < d, то a - c > b - d . Или, если a < b и c > d, то a - c < b - d . То есть, неравенства противоположного смысла можно почленно вычитать одно из другого, и брать знак неравенства, являющегося уменьшаемым.

Если a > b и m > 0, то ma > mb и a/m > b/m . То есть, обе части неравенства можно умножить или разделить на одно и то же положительное число. Неравенство при этом сохраняет свой знак.

Если a > b и m < 0, то ma < mb и a/m < b/m . То есть, обе части неравенства можно умножить или разделить на одно и то же отрицательное число. Неравенство при этом меняет свой знак на обратный.

Неравенства, содержащие неизвестные величины, подразделяются на:

¾алгебраические;

¾трансцендентные;

Алгебраические неравенства подразделяются на неравенства первой, второй, и т. д. степени.

Неравенство - алгебраическое, первой степени.

Неравенство - алгебраическое, второй степени.

Неравенство - трансцендентное.

Виды неравенства и способы их решения:

)Линейные неравенства

Пример 5: Решить неравенство

Ответ: x<-2.

2) Квадратные неравенства

Пример 6: Решить неравенство х2> 4

х2> 4

(х - 2)∙(х + 2) > 0.

Решаем методом интервалов.

) Рациональные неравенства

Пример 7: Найти все целые значения, удовлетворяющие неравенству

Методом интервалов:

Решение неравенства:

Целые числа, принадлежащие интервалу: -6;-5;-4;1.

Ответ:-6;-5;-4;1.

4) Иррациональные неравенства

Начинать решение иррациональных неравенств нужно с нахождения области определения.

Пример 8: Решить неравенство

Область определения:

Так как арифметический корень не может быть отрицательным числом, то

Ответ: [-2;7)/

) Показательные, логарифмические неравенства

Пример 9: Решите неравенство..

Пример 10: Решите неравенство.

Ответ:.

3 Особенности решения уравнения с параметрами

Рассмотрим уравнение

F(х,у,...,z;б,в,...,г)=0(1)

с неизвестными х, у, ..., z и с параметрами б,в, ..., г;при всякой допустимой системе значений параметров б0,в0, ..., г 0 уравнение (1) обращается в уравнение

F(х,у,...,z;б0,в0,...,г0)=0(2)

с неизвестными х, у,..., z, не содержащее параметров. Уравнение (2) имеет некоторое вполне определенное множество решений.

Решить уравнение содержащее параметры, это значит, для каждой допустимой системы значений параметров найти множество всех решений данного уравнения.

Основные виды уравнений с параметрами:

) Линейные и квадратные уравнения, содержащие параметр

Линейные и квадратные уравнения, содержащие параметр, можно объединить в одну группу - группу уравнений с параметром не выше второй степени.

Уравнения с параметром не выше второй степени являются самыми распространенными в практике итоговых и конкурсных заданий. Их общий вид определяется многочленом.

Контрольные значения параметра определяются уравнением. На выделенных контрольными значениями промежутках допустимых значений параметра дискриминант имеет определенный знак, соответствующие частные уравнения принадлежат одному из двух последних типов.

Тогда решением всякого уравнения с параметром не выше второй степени осуществляется по следующим этапам:

На числовой прямой отмечаются все контрольные значения параметра, для которых соответствующие частные уравнения не определены.

На области допустимых значений параметра исходного уравнения при помощи равносильных преобразований приводится к виду.

Выделяют множество контрольных значений параметра, для которых уравнение имеет конечное множество решений, то для каждого найденного контрольного значения параметра соответствующее частное уравнение решается отдельно.

Проводится классификация частных уравнений по первым трем типам. На бесконечном множестве решений уравнения проводится решение уравнения, выделяются типы бесконечных и пустых особых частных уравнений. Множеству значений параметра, для которых и, соответствует третий тип не особых частных уравнений.

Выделяются контрольные значения параметра, для которых дискриминант обращается в нуль. Соответствующие не особые частные уравнения имеют двукратный корень.

Найденные контрольные значения параметра разбивают область допустимых значений параметра на промежутки. На каждом из промежутков определяется знак дискриминанта.

) Дробно-рациональные уравнения, содержащие параметр, сводящиеся к линейным.

Процесс решения дробно-рациональных уравнений протекает по обычной схеме: данное уравнение заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего учащиеся решают известным им способом целое уравнение, исключая посторонние корни, то есть числа, которые обращают общий знаменатель в нуль. В случае уравнений с параметрами эта задача более сложная. Здесь, чтобы посторонние корни исключить, требуется находить значение параметра, обращающее общий знаменатель в нуль, то есть решать соответствующие уравнения относительно параметра.

) Иррациональные уравнения, содержащие параметр.

Главными особенностями при решении уравнений такого типа являются:

Ограничение области определения неизвестной х, так как она меняется в зависимости от значения параметра;

При рассмотрении всех особых случаев и возведении обеих частей иррационального уравнения в квадрат мы переходим к решению квадратного уравнения с параметром.

) Показательные уравнения, содержащие параметр.

Большинство показательных уравнений с параметрами сводится к показательным уравнениям вида: аf(x) = bg(х), где а>0, b>0.

Область допустимых значений такого уравнения находится как пересечение областей допустимых значений функций f(x) и g(х). Для решения уравнения аf(x) = bg(х) необходимо рассмотреть следующие случаи:

При а=b=1 решением уравнения аf(x) = bg(х) является область его допустимых значений D.

При а=1, b≠1 решением уравнения аf(x) = bg(х) служит решение уравнения g(х)=0 на области допустимых значений D.

При а≠1, b=1 решение уравнения аf(x) = bg(х) находится как решение уравнения f(х) = 0 на области D.

При а=b (а>0, а≠1, b>0, b≠1) уравнение аf(x) = bg(х) равносильно уравнению f(х) = g(х) на области D.

При а≠b (а>0, а≠1, b>0, b≠1) уравнение аf(x) = bg(х) тождественно уравнению (c>0, c≠1) на области D.

) Логарифмические уравнения, содержащие параметр.

Решение логарифмических уравнений с параметрами сводится к нахождению корней элементарного логарифмического уравнения.

Важным моментом решения уравнений такого типа является проверка принадлежности найденных корней ОДЗ исходного уравнения.

Основные методы решения уравнений, содержащих параметр:

Аналитический метод

4 Особенности решения неравенства с параметрами

Неравенство с параметрами - математическое неравенствовнешний вид и решение которого зависит от значений одного или нескольких параметров. Как при решении уравнения, так и при решении неравенства требуется найти все те значения неизвестной величины, для каждого из которых указанное соотношение оказывается верным.

Решение неравенства (уравнения) может включать в себя несколько методов решения, соответствующих каждому виду уравнения при определенных значениях параметра. Например, при каком-то значении параметра неравенство линейное, поэтому решаем его аналитически тождественными преобразованиями; при остальных значениях параметра неравенство квадратичное, - решаем его функционально-графическим способом.

Аналогично уравнениям с параметрами, неравенства с параметрами имеют ту же классификацию видов и методов решения.

) Линейные и квадратные неравенства, содержащие параметр

) Дробно-рациональные неравенства, содержащие параметр, сводящиеся к линейным.

Решение некоторых дробно-рациональных неравенств сводится к решению неравенств первой или второй степени.

) Иррациональные неравенства, содержащие параметр.

) Показательные неравенства, содержащие параметр.

) Логарифмические неравенств, содержащие параметр.

Основные методы решения неравенств, содержащих параметр:

Аналитический метод

Свойства функций в задачах, содержащих параметр. Функциональный подход.

Графический метод. Координатная плоскость (x;y).

Графический метод. Координатная плоскость (x;a).

Решение задач с параметрами является одним из самых трудных разделов школьной математики. При решении задач с параметрами требуется, кроме хорошего знания стандартных методов решений уравнений и неравенств, умение проводить довольно разветвленные логические построения, аккуратность и внимательность для того, чтобы не потерять решений и не приобрести лишних. Это требует от школьника более развитого логического мышления и математической культуры, но, в свою очередь, эти задачи сами способствуют их развитию. Опыт вступительных экзаменов показывает, что учащиеся, владеющие методами их решения, обычно успешно справляются и с другими задачами.

К сожалению, в программах по математике для неспециализированных школ задачам с параметром практически не отводится места, а, например, в учебнике для учащихся школ и классов с углубленным изучением курса математики («Алгебра и математический анализ для 10 и 11 классов», Н.Я. Виленкин, О.С. Ивашев-Мусатов, С.И. Шварцбурд) им отведено место только в 11-м классе. Между тем, задачи с параметрами можно и нужно использовать уже начиная с линейных и квадратных уравнений и неравенств. Это могут быть задачи нахождения решений в общем виде, определения корней, удовлетворяющих каким-либо свойствам, исследования количества корней в зависимости от значений параметра. Так сделано в «Сборнике задач по алгебре для 8-9 классов», 1994 г. (авторы: М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич). Важно, чтобы школьники уже на первых простых примерах усвоили: во-первых, необходимость аккуратного обращения с параметром - фиксированным, но неизвестным числом, поняли, что оно имеет двойственную природу (с одной стороны, это некоторое число, с другой стороны, степень свободы общения с ним ограничивается его неизвестностью); во-вторых, что запись ответа существенно отличается от записи ответов аналогичных уравнений и неравенств без параметра.

Методически было бы правильно каждый пройденный тип уравнений (неравенств) завершать задачами с использованием параметра. Во-первых, школьнику трудно привыкнуть к параметру за два-три занятия - нужно время; во-вторых, использование подобных задач улучшает закрепление пройденного материала; в-третьих, оно способствует развитию его математической и логической культуры, а также развитию интереса к математике, поскольку открывает перед ним новые методы и возможности для самостоятельного поиска.

Понятие параметра является математическим понятием, которое часто используется в школьном курсе математики и в смежных дисциплинах.

класс - при изучении линейной функции и линейного уравнения с одной переменной.

класс - при изучении квадратных уравнений.

Общеобразовательная программа школьного курса математики не предусматривает решение задач с параметрами, а на вступительных к заменах в вузы и на ЕГЭ по математике задачи с параметрами присутствуют, решение которых вызывает большие затруднения учащихся.Задачи с параметрами обладают диагностической и прогностической ценностью, которые позволяют проверить знания основных разделов школьного курса математики, уровень логического мышления, первоначальные навыки исследовательской деятельности.

При решении уравнения (неравенства) можно пользоваться следующим алгоритмом.

Алгоритм решения уравнения или неравенства с параметром

1. Определяют ограничения, налагаемые на значения неизвестного и параметра, вытекающие из того, что функции и арифметические операции в или имеют смысл.

Определяют формальные решения, записываемые без учета ограничений. Если при решении возникают контрольные значения параметра, то их наносят на числовую ось. Эти значения разбивают область допустимых значений параметра на подмножества. На каждом из подмножеств решают заданное уравнение..

Исключают те значения параметра, при которых формальные решения не удовлетворяют полученным ограничениям.

На числовую ось. добавляют значения параметра, найденные в п.3. Для каждого из промежутков на оси. записывают все полученные решения в зависимости от значений параметра. (В случае достаточно простых уравнений п.4 можно опустить).

Выписывают ответ, т.е. записывают решения в зависимости от значений параметра.

Наличие параметра в задаче предполагает специальную форму записи ответа, позволяющую установить, каков ответ для любого допустимого значения параметра. Недопустимые значения также указываются в ответе, и считается, что при этих значениях параметра задача не имеет решения. При записи ответа обычно значения параметра перечисляются в порядке возрастания от −∞ до +∞, но иногда для компактности ответа объединяют промежутки для параметра, на которых формулы решения совпадают.

В случае ветвления решения удобно использовать числовую прямую., на которую наносятся контрольные значения параметра, а на промежутках, на которые эти значения разбили прямую, указываются ответы задачи. Данный прием позволяет в дальнейшем не потерять найденные ответы и четко указать значения параметра, которым они соответствуют.

Продемонстрируем сказанное выше на примере.

Пример 10: Решить неравенство.

Контрольные значения параметра получаются из условия, так как при неравенство не содержит переменной x.

Нанесем на числовую ось Oa контрольные значения. Они разбивают ось Oa на промежутки:

) a<0; 2) 0< a <2; 3) a>2

На каждом из этих промежутков решим данное неравенство. Значения a=0 и. a=2 требуют отдельного рассмотрения.

Если a<0, то a(a-2)>0. Разделив обе части неравенства на множитель a(a − 2) ≠ 0 , получим x>.

Если 2>a>0, a(a − 2) < 0 и, следовательно, x<.

Если a>2, a(a − 2) > 0 и x>/

Нанесем получаемые в ходе решения ответы на соответствующие промежутки числовой оси Oa и запишем ответ.

Промежуток, к которому относится соответствующее решение, помечается на рисунке дугой. На ее конце ставится стрелочка в том случае, если это решение не относится к крайней точке промежутка.

Ответ: Если a<0, то x>; если 02, то x>; если a=0 и a=2, то решений нет.

Главная особенность задач с параметрами - ветвления решения в зависимости от значений параметров. Другими словами, процесс решения осуществляется классификаций частных уравнений (неравенств) по типам с последующим поиском решений каждого типа.

Одновременно решение бесконечной совокупности частных уравнений и неравенств с учетом требования равносильности преобразований возможно лишь при развитии достаточного уровня логического мышления. С другой стороны, формирование методов решения уравнений и неравенств с параметрами обеспечивает значительный процесс в развитии математической культуры учащихся. Развивающий характер уравнений и неравенств с параметрами определяется их способностью реализовывать многие виды мыслительной деятельности учащихся:

Выработка определенных алгоритмов мышления.

Умение определить наличие и количество корней в уравнении.

Решение семейств уравнений, являющихся следствием данного.

Выражение одной переменной через другую.

Повторение большого объема формул при решении.

Значение соответствующих методов решения.

Широкое применение словесной и графической аргументации.

Развитие графической культуры учащихся.

Все вышесказанное позволяет говорить о необходимости изучения решений задач с параметрами.

уравнение неравенство параметр

Заключение

Таким образом, в нашей курсовой работе речь шла о уравнениях и неравенствах с параметрами в школьном курсе математике, особенности их решения. Были рассмотрены уравнения и неравенства в школьном курсе математике, особенности решения уравнений и неравенств с параметрами.Была разработана методики к решению уравнений и неравенств с параметрами.

Цель нашей курсовой работы заключалась в выявление видов, методов решения уравнений и неравенств с параметрами.

Для достижения данной цели, была подобрана и изучена литература по данной проблеме, исследовано особенности решения уравнений и неарвенств с параметрамишкольном курсе математики основной школы, представлена методические рекомендации к решению уравнений(неравенств) с параметрами.

Вывод: Задачи с параметрами являются самыми сложными из всех заданий школьного курса математики. Для их решения требуется умение мыслить логически: необходимо в каждый момент проведения решения достаточно отчётливо представлять себе, что уже сделано, что ещё надо сделать, что означают уже полученные результаты. В заданиях ЕГЭ по математике проверяется умение выпускника мыслить сжато, логично и аргументировано.

Изучение уравнений и неравенств с параметрами в общеобразовательных школах дает учащимся большие возможности для анализа различных ситуаций, то есть показывает значимость этих понятий при решении многих практических задач. Именно с простейших практических задач и приложений математически постепенно формируется у школьников понимание значимости математики в жизни.

Список используемой литературы

уравнение неравенство математика

1.Алгебра. 7 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2010.

2.Алгебра. 7 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2010.

3.Алгебра. 7 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011.

Алгебра. 8 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2012.

Алгебра. 8 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2011.

Алгебра. 8 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011.

Алгебра. 9 класс: Учеб.для общеобразовательных учеб. заведений / К.С. Муравин, Г.К. Муравин, Г.В. Дорофеев. - М.: Дрофа, 2013.

Алгебра. 9 класс: В двух частях. Ч. 1: Учебник для общеобразоват. учреждений / А.Г. Мордкович. - М.: Мнемозина, 2013.

Алгебра. 9 класс: Учебник для общеобразоват. учреждений / С.М. Никольский, М.К. Потапов и др. - М.: Просвещение, 2011.

Алгебра. Учеб.для 7 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2011.

Алгебра. Учеб.для 7 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2012.

Алгебра. Учеб.для 8 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2014.

Алгебра. Учеб.для 8 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2011.

Алгебра. Учеб.для 9 класса средней школы / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. Теляковского. - М.: Просвещение, 2010.

Алгебра. Учеб.для 9 класса средней школы /Ш.А. Алимов, Ю.М. Колягин и др. - М.: Просвещение, 2001.

Беляева Э.С. Математика. Уравнение и неравенство с параметрами в 2 ч.: Учебное пособие/ Беляева Э.С., Потапов А.С., Титоренко С.А. -., - М.:,2009.

Крамор В.С. Задачи с параметром и методы их решения: Учебное пособие /- М.: Оникс; Мир и Образование,2007

Козко А.И. Задачи с параметрами и другие сложные задачи: Учебное пособие для вузов/Козко А. И.,Чирский В. Г. - М.:,МЦНМО,2007.

Мирошин В.В. Решение задач с параметрами. Теория и практика: Учебное пособие /. - М.: Экзамен,2009.

Прокофьев А.А. Задачи с параметрами: Учебное пособие. - М.: МИЭТ, 2004.

Севрюков П.Ф. Школа решения задач с параметрами: Учебное пособие /Севрюков П.Ф., Смоляков А. Н.-2-е изд.- М.:,2009.

Класс: 11

Цели:

Образовательная:

• систематизировать и обобщить знания о решении уравнения с параметром;
• показать основные приемы решения таких уравнений.

Развивающая: расширить и углубить изучение различных приемов решения уравнений с параметром.

Воспитательная: показать значимость зависимости ответа в задаче с параметром от выбранного значения параметра.

Используемые методы обучения – их применение .

• Объяснительно-иллюстративный.
• Обобщения, аналогии и сравнения.
• УДЕ – создание ключевых задач, аналогия изображений на плоскости.
• Интегрированный – сопоставление алгебры и геометрические интерпретации, слайды.

Формирование общеучебных умений и навыков:

• Выделение существенных признаков изучаемых объектов;
• Выработка практических навыков;
• Используемые методы работы с аудиторией: работа в диалоговом режиме;
• Психологические аспекты урока;
• Создание комфортной рабочей атмосферы;
• Побуждение к активной диалоговой деятельности.

Ход урока

Введение . Вступительное слово учителя .

Уравнения стали привычной частью вариантов вступительных экзаменов ЕГЭ.

Уравнения с параметром вызывают серьезные трудности логического характера.
Каждое такое уравнение – это, по существу, краткая запись семейства уравнений. Ясно, что выписать каждое уравнение из бесконечного семейства невозможно, но тем не менее каждое из них должно быть решено. Поэтому возникает необходимость в рассмотрении системы понятий и поиске методов решения уравнений с параметрами (линейных, рациональных и т.д.)

Пусть дано уравнение F(х;а) = 0. Если придать параметру а какое – либо фиксированное значение, то данное уравнение можно рассматривать как «обычное» уравнение с одной переменной.

Поставим задачу : Выяснить, какой может быть ситуация при выбранном значении параметра?

Работа с учащимися в диалоговом режиме.

Обозначим основные проблемы:

1. Установить основные понятия уравнений с параметрами.
2. Для каждого вида уравнений школьного курса математики установить общий метод решения соответствующих уравнений с параметрами – единый как для одного, так и для двух параметров.
3. Рассмотреть примеры заданий на исследование уравнений.
4. Каково установление числа корней уравнений.
5. Нахождение общего корня двух уравнений – в чем его суть?
6. Геометрические интерпретации.

I этап – решение первой проблемы .

Работа с учащимися в диалоговом режиме .

Какие вопросы вы себе определите для установления основных понятий?

Что такое задача с параметром? Что является областью допустимых значений параметра? Что значит решить задачу с параметром? Сколько видов задач с параметрами существует? Что необходимо учитывать при их решении?

Появляется слайд и конспект - Задача с параметром – это множество задач, каждая из которых получается из условия подстановкой конкретного значения параметра. - Область допустимых значений параметра – это множество значений параметра, при подстановке которых получается задача, имеющая смысл. - Решить задачу с параметром означает для любого допустимого значения параметра найти множество всех решений данной задачи. - Рассматривать мы с вами будем задачи с параметром двух основных типов. В задачах I типа требуется для каждого значения параметра решить задачу. Для этого необходимо: разбить ОДЗ параметра на части, на каждой из которых задачу можно решить одним и тем же способом; на каждой из полученных частей решить задачу. В задачах II типа требуется найти все значения параметра, при которых выполнены те или иные заданные условия. - Ответ в задаче с параметром – это описание множества ответов к задачам, полученных при конкретных значениях параметра.

Например.

1) Решить уравнение а (а – 1) = а – 1.

Решение . Перед нами линейное уравнение, имеющее смысл при всех допустимых значениях а. Будем решать его «как обычно»: делим обе части уравнения на коэффициент при неизвестном. Но всегда ли возможно деление?

Делить на ноль нельзя. Придется рассмотреть отдельно случай, когда коэффициент при неизвестном равен о. Получим:

Ответ: 1) если а 0, а 1, то х = ;

2) если а = 1, то х – любое число;

3) если а = 0, то корней нет.

2) Решить уравнение (а – 1)х 2 + 2 (2а – 1)х + 4 а + 3 = 0.

Решение . Рассмотрим два случая:

Рассмотрим дискриминант: D = (2а – 1) 2 – (а – 1)(4а + 3) = - 3а + 4.

Если же а , то х 1,2 = .

Ответ: 1) если а > , то корней нет;

2) если а = 1, то х = - 3,5;

3) если а и а1, то х 1,2 = .

II этап – решение второй проблемы .

Рассмотрим способ классификации частных уравнений с помощью модели общих решений.
Появляется слайд.

Например. В рациональном уравнении функция f 1 (а) = является общим решением для тех значений параметра, для которых . Поскольку

общее решение уравнения на А f1 = }.

Функция f 2 (а) = есть общее решение уравнения на множестве А f2 = .
Построим модель общих решений в следующем виде

На модели выделяем все типы частных уравнений: ; ; .

Итак, на примерах рассмотрены основные понятия уравнений с параметрами: область допустимых значений; область определения; общие решения; контрольные значения параметров; типы частных уравнений.

На базе введенных параметров определим общую схему решения всякого уравнения F(а;х) = 0 с параметром а (для случая двух параметров схема аналогична):

• устанавливается область допустимых значений параметра и область определения;
• определяются контрольные значения параметра, разбивающие область допустимых значений параметра на области однотипности частных уравнений;
• для контрольных значений параметра соответствующие частные уравнения исследуются отдельно;
• находятся общие решения х = f 1 (а), …, f k (а) уравнения F(а;х) =0 на соответствующих множествах А f1 , ……, А fk значений параметра;
• составляется модель общих решений, контрольных значений параметра в следующем виде (на слайде);

• на модели выделяются промежутки значений параметра с одинаковыми решениями (области однотипности);
• для контрольных значений параметра и выделенных областей однотипности записываются характеристики всех типов частных решений.

III этап – примеры заданий на исследование уравнений.

Рассмотрим примеры решения задач с параметрами 2 типа.

Особенно часто встречаются задачи на расположение корней квадратного уравнения. При их решении хорошо «работают» графические иллюстрации. Расположение корней относительно заданных точек плоскостью определяется направлением ветвей соответствующей параболы, координатами вершины, а также значениями в заданных точках.

Например.

1) При каких значениях параметра а уравнение (а 2 + а + 1)х 2 + (2а – 3)х + а – 5 = 0 имеет два корня, один из которых больше 1, а другой меньше 1?

Решение . Пусть f(х) = (а 2 + а + 1)х 2 + (2а – 3)х + а – 5. Так как а 2 + а + 1 >0, то для квадратичной функции f(х) условие задачи может выполняться только при условии f (х) < 1.

Решая неравенство f(1) = а 2 + 4а – 7 < 0, получим, что -2 - < а < - 2 + .

Ответ : -2 - < а < - 2 + .

2) При каких значениях параметра m корни уравнения (m – 1)х 2 – 2 mх + m + 3 = 0 положительны?

Решение . Пусть f(х) = (m-1)х 2 - 2 mх + m + 3 тогда:

1) если, m = 1,то -2х + 4=0, х= 2- корень положителен;

2) если m 1, то с помощью рисунка можно получить следующие соотношения:

Рассмотрим 2 случая:

1) если 1,5 m > 0, тогда из 2 и 3 неравенств последней системы получим, что m > 1, т.е. окончательно 1,5 m > 1;

2) если m < 0, тогда из неравенства (m-1)m > 0 получим, что m-1 < 0, откуда m + 3 < 0, т.е. окончательно m < -3.

Ответ : m (-; -3)

IV этап - рассмотрим задачи на установления числа корней уравнения.

Пример 1. При каких значениях параметра, а уравнение 2 cos 2 x – (2а + 9)cosx + 9а = 0 не имеет корней.

Решение. Пусть у = cosх, тогда исходное уравнение примет вид 2у 2 – (2 а + 9)у + 9а = 0, корни которого у 1 = а, у 2 = 4,5. Уравнение cosх = 4,5 корней не имеет, а уравнение cosх = а не имеет корней, если > 1.

Ответ : (- ; -1) (1; ).

Пример 2 . Найдите все значения параметра а, при которых уравнение не имеет корней.

Решение . Данное уравнение равносильно системе: .

Уравнение не имеет решения в двух случаях: а = и

Пример 3 . При каких значениях параметра а уравнение имеет единственное решение?

Решение . Решение уравнения может быть единственным только, если х = 0. Если х = 0,то а 2 -1 = 0, и а = 1.

Рассмотрим 2 случая:

1) если а = 1, то х 2 - = 0 – корней три;

2). Если а = -1, то то х 2 + = 0, х = 0 - единственный корень.

Пример 4. При каких значениях параметра а уравнение имеет 2 корня?

Решение. Данное уравнение равносильно системе: . Выясним, когда квадратное уравнение х 2 – х – а = 0 имеет 2 неотрицательных корня.

Полученное уравнение имеет два корня, если 1+ 4а > 0; они неотрицательны, если

0 > а > - .

Ответ : (- ; 0] .

Во многих случаях при установлении числа корней уравнении имеет значение симметрия.

V этап - нахождение общего корня двух уравнений.

Пример 1. При каких значениях параметра а уравнение х 2 + 3х + 7а -21 =0 и х 2 +6х +5а -6 =0 имеют общий корень?

Решение. Исключим параметр а из полученной системы. Для этого первое уравнение умножим на -5, второе - на7, а результаты сложим. Получим: 2х 2 + 27х +63 =0, корни которого х 1 = -3, х 2 = -10,5. Подставим корни в одно из уравнений и найдем значение параметра а.

Ответ : 3 и – 8,25.

Пример 2. При каких значениях параметра а уравнение х 2 – ах + 2 = 0 и 3х 2 + (а - 9)х+ 3=0 равносильны?

Решение . Как известно уравнения равносильны, если множество их корней совпадают. Рассмотрим 2 случая.

1) Уравнения не имеют корней (множество корней пусто). Тогда их дискриминанты отрицательны:

Система неравенств решений не имеет.

2) Уравнения имеют общие корни. Тогда

Следовательно, данные уравнения могут иметь общие корни только при а = 3 или а = .

Проверить самостоятельно!

VI этап – геометрические интерпретации.

Решение задач с параметрами может существенно облегчить использование графиков.

Пример 1 . Решите уравнение в зависимости от параметра а: .

Решение. Понятно что при а 0:

Все ли корни подходят. Чтобы это выяснить, построим график функции а =.
Количество корней можно увидеть на рисунке:

1. если а < 0, то корней нет;
2. если а = 0 и а > 0, то 2 корня.

Найдем эти корни.

При а = 0 получим х 2 – 2х – 3 = 0 и х 1 = -1, х 2 = 3; при а > 4 это корни уравнения х 2 – 2х – 3 – а = 0.

Если 0 < а < 4 – все 4 корня подходят.

Если а = 4 – три корня:
Ответ : 1) если а < 0, то корней нет;

2) если а = 0, то х 1 = -1, х 2 =3;

3) если 0 < a < 4, то х 1,2,3.4 = 1 ;

4) если а = 4, то х 1 = 1; х 2,3 = 1 ;

5) если а > 4, то х 1,2 = 1 .

Пример 2 . При каких значениях а уравнение имеет более двух корней?

Решение . Если подставить х = 0 в исходное уравнение, то получим 6 = 6, это означает, что х = 0 является решением уравнения при любом а.

Пусть теперь х 0, тогда можно записать . Выясним знаки выражений 2х + 3 и 2х – 3.

Раскроем модули: а = (1)

В плоскости х0а построим множество точек (х;а), координаты которых удовлетворяют соотношению (1).

Если а = 0, то уравнение имеет бесконечное множество решений на промежутке , при других значениях а число решений уравнения не превышает двух.

Ответ : а = 0.

Тестовый контроль

1 вариант	2 вариант
1) Решите уравнение: 0 · х = а Ответы	1) Решить уравнение: а х = а. Ответы : а) при а ≠ 0, х = 1, при а = 0, х R б) при а = 0, х R, при а ≠ 0 корней нет в) при а = 0 нет корней, при а ≠ х =
2) Решит уравнение: (в – 2)·х = 5 + в. Ответы:	2) Решите уравнение (в + 1)·х = 3 – в . Ответы: а) при в = 2 нет корней; при в ≠2, х = ; б) при в = -2 нет корней, при в ≠-2 х = в) при в = -1 нет корней, при а ≠ - 1
3) При каких значениях параметра с уравнение имеет бесконечное множество решений? с·(с + 1)·х = с 2 – 1 . Ответ : а) при с = -1, х R, ; Чаплыгин В.Ф., Чаплыгина Н.Б. Задачи с параметрами по алгебре и анализу, 1998 г.

Государственное бюджетное общеобразовательное учреждение

Самарской области средняя общеобразовательная

школа № 2 им. В. Маскина ж.-д. ст. Клявлино

муниципального района Клявлинский

Самарской области

« Уравнения

и

неравенства

с параметрами»

учебное пособие

Клявлино

Учебное пособие

« Уравнения и неравенства с параметрами» для учащихся 10 –11 классов

данное пособие является приложением к программе элективного курса «Уравнения и неравенства с параметрами», которая прошла внешнюю экспертизу (научно-методическим экспертным советом министерства образования и науки Самарской области от 19 декабря 2008 года бала рекомендована к использованию в образовательных учреждениях Самарской области)

Авторы

Ромаданова Ирина Владимировна

учитель математики МОУ Клявлинской средней общеобразовательной

школы № 2 им. В.Маскина Клявлинского района Самарской области

Сербаева Ирина Алексеевна

Введение……………………………………………………………3-4

Линейные уравнения и неравенства с параметрами……………..4-7

Квадратные уравнения и неравенства с параметрами……………7-9

Дробно- рациональные уравнения с параметрами……………..10-11

Иррациональные уравнения и неравенства с параметрами……11-13

Тригонометрические уравнения и неравенства с параметрами.14-15

Показательные уравнения и неравенства с параметрами………16-17

Логарифмические уравнения и неравенства с параметрами…...16-18

Задачи ЕГЭ………………………………………………………...18-20

Задания для самостоятельной работы…………………………...21-28

Введение.

Уравнения и неравенства с параметрами.

Если в уравнении или неравенстве некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Для того, чтобы решить уравнение или неравенство с параметрами необходимо:

Выделить особое значение - это то значение параметра, в котором или при переходе через которое меняется решение уравнения или неравенства.

Определить допустимые значения – это значения параметра, при которых уравнение или неравенство имеет смысл.

Решить уравнение или неравенство с параметрами означает:

1) определить, при каких значениях параметров существуют решения;

2) для каждой допустимой системы значений параметров найти соответствующее множество решений.

Решить уравнение с параметром можно следующими методами: аналитическим или графическим.

Аналитический метод предполагает задачу исследования уравнения рассмотрением нескольких случаев, ни один из которых нельзя упустить.

Решение уравнения и неравенства с параметрами каждого вида аналитическим методом предполагает подробный анализ ситуации и последовательное исследование, в ходе которого возникает необходимость «аккуратного обращения» с параметром.

Графический метод предполагает построение графика уравнения, по которому можно определить, как влияет соответственно, на решение уравнения изменение параметра. График подчас позволяет аналитически сформулировать необходимые и достаточные условия для решения поставленной задач. Графический метод решения особенно эффективен тогда, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра и обладает несомненным преимуществом увидеть это наглядно.

§ 1. Линейные уравнения и неравенства.

Линейное уравнение а x = b , записанное в общем виде, можно рассматривать как уравнение с параметрами, где x – неизвестное, a , b – параметры. Для этого уравнения особым или контрольным значением параметра является то, при котором обращается в нуль коэффициент при неизвестном.

При решении линейного уравнения с параметром рассматриваются случаи, когда параметр равен своему особому значению и отличен от него.

Особым значением параметра a является значение а = 0.

b = 0 является особым значением параметра b .

При b ¹ 0 уравнение решений не имеет.

При b = 0 уравнение примет вид: 0х = 0 . Решением данного уравнения является любое действительное число.

Неравенства вида ах > b и ax < b (а ≠ 0) называются линейными неравенствами. Множество решений неравенства ах > b – промежуток

(; +), если a > 0 , и (-;) , если а < 0 . Аналогично для неравенства

ах < b множество решений – промежуток (-;), если a > 0, и (; +), если а < 0.

Пример 1. Решить уравнение ах = 5

Решение : Это линейное уравнение.

Если а = 0 , то уравнение 0 × х = 5 решения не имеет.

Если а ¹ 0, х = - решение уравнения.

Ответ : при а ¹ 0, х=

при а = 0 решения нет.

Пример 2. Решить уравнение ах – 6 = 2а – 3х.

Решение: Это линейное уравнение, ах – 6 = 2а – 3х (1)

ах + 3х = 2а +6

Переписав уравнение в виде (а+3)х = 2(а+3) , рассмотрим два случая:

а= -3 и а ¹ -3.

Если а= -3 , то любое действительное число х является корнем уравнения (1). Если же а ¹ -3 , уравнение (1) имеет единственный корень х = 2.

Ответ: При а = -3, х R ; при а ¹ -3, х = 2.

Пример 3. При каких значениях параметра а среди корней уравнения

2ах – 4х – а 2 + 4а – 4 = 0 есть корни больше 1 ?

Решение : Решим уравнение 2ах – 4х – а 2 + 4а – 4 = 0 – линейное уравнение

2(а - 2) х = а 2 – 4а +4

2(а - 2) х = (а – 2) 2

При а = 2 решением уравнения 0х = 0 будет любое число, в том числе и большее 1.

При а ¹ 2 х =
. По условию х > 1 , то есть
>1, а > 4.

Ответ: При а {2} U (4;∞).

Пример 4 . Для каждого значения параметра а найти количество корней уравнения ах=8.

Решение. ах = 8 – линейное уравнение.

y = a – семейство горизонтальных прямых;

y = - графиком является гипербола. Построим графики этих функций.

Ответ: Если а =0 , то уравнение решений не имеет. Если а ≠ 0 , то уравнение имеет одно решение.

Пример 5 . С помощью графиков выяснить, сколько корней имеет уравнение:

|х| = ах – 1.

y =| х | ,

y = ах – 1 – графиком является прямая, проходящая через точку (0;-1).

Построим графики этих функций.

Ответ:При|а|>1 - один корень

при | а| ≤1 – уравнение корней не имеет.

Пример 6 . Решить неравенство ах + 4 > 2х + а 2

Решение : ах + 4 > 2х + а 2
(а – 2) х > а 2 – 4. Рассмотрим три случая.

Ответ. х > а + 2 при а > 2; х <а + 2, при а < 2; при а=2 решений нет.

§ 2. Квадратные уравнения и неравенства

Квадратное уравнение – это уравнение вида ах ² + b х + с = 0 , где а≠ 0,

а, b , с – параметры.

Для решения квадратных уравнений с параметром можно использовать стандартные способы решения на применение следующих формул:

1 ) дискриминанта квадратного уравнения: D = b ² - 4 ac , (
²- ас)

2) формул корней квадратного уравнения: х 1 =
, х 2 =
,

(х 1,2 =
)

Квадратными называются неравенства вида

a х 2 + b х + с > 0, a х 2 + b х + с< 0, (1), (2)

a х 2 + b х + с ≥ 0, a х 2 + b х + с ≤ 0, (3), (4)

Множество решений неравенства (3) получается объединением множеств решений неравенства (1) и уравнения , a х 2 + b х + с=0. Аналогично находится множество решений неравенства (4).

Если дискриминант квадратного трехчлена a х 2 + b х + с меньше нуля, то при а >0 трехчлен положителен при всех х R .

Если квадратный трехчлен имеет корни (х 1 < х 2 ), то при а > 0 он положителен на множестве (-; х 2 )
(х 2; +) и отрицателен на интервале

(х 1 ; х 2 ). Если а < 0, то трехчлен положителен на интервале (х 1 ; х 2 ) и отрицателен при всех х (-; х 1 )
(х 2; +).

Пример 1. Решить уравнение ах² - 2 (а – 1)х – 4 = 0 .

Это квадратное уравнение

Решение : Особое значение а = 0.

При а = 0 получим линейное уравнение 2х – 4 = 0 . Оно имеет единственный корень х = 2.

При а ≠ 0. Найдем дискриминант.

D = (а-1)² + 4а = (а+1)²

Если а = -1, то D = 0 – один корень.

Найдем корень, подставив вместо а = -1.

-х² + 4х – 4= 0, то есть х² -4х + 4 = 0, находим, что х=2.

Если а ≠ - 1 , то D >0 . По формуле корней получим: х=
;

х 1 =2, х 2 = -.

Ответ: При а=0 и а= -1 уравнение имеет один корень х = 2; при а ≠ 0 и

а ≠ - 1 уравнение имеет два корня х 1 =2, х 2 =-.

Пример 2. Найдите количество корней данного уравнения х²-2х-8-а=0 в зависимости от значений параметра а.

Решение. Перепишем данное уравнение в виде х²-2х-8=а

y = х²-2х-8 - графиком является парабола;

y =а - семейство горизонтальных прямых.

Построим графики функций.

Ответ: При а <-9 , уравнение решений не имеет; при а=-9, уравнение имеет одно решение; при а>-9 , уравнение имеет два решения.

Пример 3. При каких а неравенство (а – 3) х 2 – 2ах + 3а – 6 >0 выполняется для всех значений х?

Решение. Квадратный трехчлен положителен при всех значениях х, если

а-3 > 0 и D <0, т.е. при а, удовлетворяющих системе неравенств

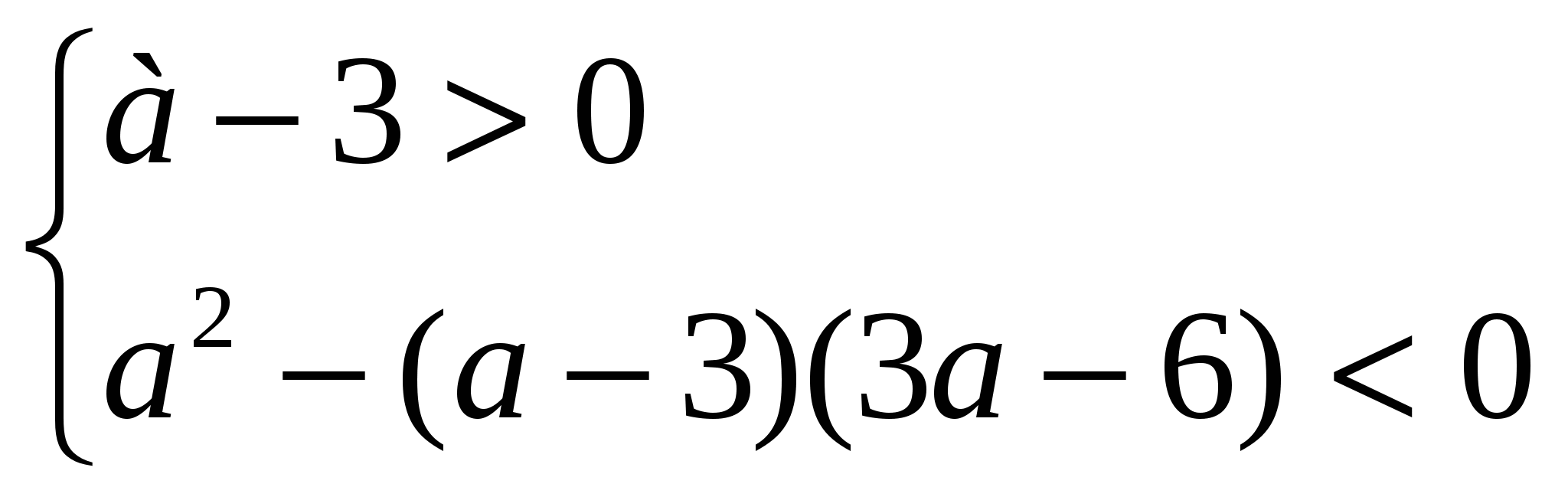
, откуда следует, что a > 6 .

Ответ. a > 6

§ 3. Дробно- рациональные уравнения с параметром,

сводящиеся к линейным

Процесс решения дробных уравнений выполняется по обычной схеме: дробное заменяется целым путем умножения обеих частей уравнения на общий знаменатель левой и правой его частей. После чего решается целое уравнение, исключая посторонние корни, то есть числа, которые обращают знаменатель в нуль.

В случае уравнений с параметром эта задача более сложная. Здесь, чтобы «исключить» посторонние корни, требуется найти значение параметра, обращающее общий знаменатель в нуль, то есть решить соответствующие уравнения относительно параметра.

Пример 1. Решить уравнение
= 0

Решение: Д.З: х +2 ≠ 0 , х ≠ -2

х – а = 0, х = а.

Ответ: При а ≠ - 2, х=а

При а = -2 корней нет.

Пример 2 . Решить уравнение
-
=
(1)

Это дробно- рациональное уравнение

Решение: Значение а = 0 является особым. При а = 0 уравнение теряет смысл и, следовательно, не имеет корней. Если а ≠ 0, то после преобразований уравнение примет вид: х² + 2 (1-а) х + а² - 2а – 3 = 0 (2) – квадратное уравнение.

Найдем дискриминант = (1 – а)² - (а² - 2а – 3)= 4, находим корни уравнения х 1 = а + 1, х 2 = а - 3.

При переходе от уравнения (1) к уравнению (2) расширилась область определения уравнения (1), что могло привести к появлению посторонних корней. Поэтому, необходима проверка.

П р о в е р к а. Исключим из найденных значений х такие, при которых

х 1 +1=0, х 1 +2=0, х 2 +1=0, х 2 +2=0.

Если х 1 +1=0, то есть (а+1) + 1= 0 , то а= -2. Таким образом,

при а= -2 , х 1 -

Если х 1 +2=0, то есть (а+1)+2=0, то а = - 3 . Таким образом, при а = - 3, х 1 - посторонний корень уравнения. (1).

Если х 2 +1=0, то есть (а – 3) + 1= 0 , то а = 2 . Таким образом, при а = 2 х 2 - посторонний корень уравнения (1).

Если х 2 +2=0, то есть (а – 3) + 2 = 0, то а=1 . Таким образом, при а = 1,

х 2 - посторонний корень уравнения (1).

В соответствии с этим при а = - 3 получаем х = - 3 – 3 = -6 ;

при а = - 2 х = -2 – 3= - 5;

при а = 1 х =1 + 1= 2;

при а = 2 х=2+1 = 3.

Можно записать ответ.

Ответ: 1) если а= -3, то х= -6; 2) если а= -2 , то х= -5 ; 3) если а= 0 , то корней нет; 4) если а= 1 , то х= 2; 5) если а=2 , то х=3 ; 6) если а ≠ -3, а ≠ -2, а ≠ 0, а≠ 1, а ≠ 2, то х 1 = а + 1, х 2 = а-3.

§4. Иррациональные уравнения и неравенства

Уравнения и неравенства, в которых переменная содержится под знаком корня, называется иррациональным.

Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения в степень обеих частей уравнения или замены переменной. При возведении обеих частей уравнения в четную степень возможно появление посторонних корней. Поэтому при использовании указанного метода следует проверить все найденные корни подстановкой в исходное уравнение, учитывая при этом изменения значений параметра.

Уравнение вида
=g (x ) равносильно системе

Неравенство f (x ) ≥ 0 следует из уравнения f (x ) = g 2 (x ).

При решении иррациональных неравенств будем использовать следующие равносильные преобразования:

≤ g(x)


≥g(x)

Пример 1. Решите уравнение
= х + 1 (3)

Это иррациональное уравнение

Решение: По определению арифметического корня уравнение (3) равносильно системе
.

При а = 2 первое уравнение системы имеет вид 0 х = 5 , то есть не имеет решений.

При а≠ 2 х=
. Выясним, при каких значениях а найденное значение х удовлетворяет неравенству х ≥ -1:
≥ - 1,
≥ 0,

откуда а ≤ или а > 2.

Ответ: При а≤, а > 2 х=
, при < а ≤ 2 уравнение решений не имеет.

Пример 2. Решить уравнение
= а (приложение 4)

Решение. y =

y = а – семейство горизонтальных прямых.

Построим графики функций.

Ответ : при а<0 –решений нет;

при а ≥ 0 – одно решение.

Пример 3 . Решим неравенство (а+1)
<1.

Решение. О.Д.З. х ≤ 2 . Если а+1 ≤0 , то неравенство выполняется при всех допустимых значениях х . Если же а+1>0 , то

(а+1)
<1.

<

откуда х (2-
2

Ответ. х (- ;2 при а (-;-1, х (2-
2

при а (-1;+).

§ 5. Тригонометрические уравнения и неравенства.

Приведем формулы решений простейших тригонометрических уравнений:

Sinx = a
x= (-1) n arcsin a+πn, n Z, ≤1, (1)

Cos x = a
x = ±arccos a + 2 πn, n Z, ≤1. (2)

Если >1, то уравнения (1) и (2) решений не имеют.

tg x = a
x= arctg a + πn, n Z, aR

ctg x = a
x = arcctg a + πn, n Z, aR

Для каждого стандартного неравенства укажем множество решений:

1. sin x > a
arcsin a + 2 πn Z,

при a <-1, xR ; при a ≥ 1, решений нет.

2. . sin x < a
π - arcsin a + 2 πnZ,

при а≤-1, решений нет; при а >1, xR

3. cos x > a
- arccos a + 2 πn < x < arccos a + 2 πn , n Z ,

при а<-1, xR ; при a ≥ 1 , решений нет.

4. cos x arccos a+ 2 πnZ,

при а≤-1 , решений нет; при a > 1, x R

5. tg x > a, arctg a + πnZ

6. tg x < a, -π/2 + πn Z

Пример1. Найти а , при которых данное уравнение имеет решение:

Cos 2 x + 2(a-2)cosx + a 2 – 4a – 5 =0.

Решение. Запишем уравнение в виде

с os 2 x + (2 a -4) cosx +(a – 5)(а+1) =0, решая его как квадратное, получаем cosx = 5-а и cosx = -а-1.

Уравнение cosx = 5- а имеет решения при условии -1≤ 5- а ≤1
4≤ а ≤ 6, а уравнение cosx = - а-1 при условии -1≤ -1- а ≤ 1
-2 ≤ а ≤0.

Ответ. а -2; 0
4; 6

Пример 2. При каких b найдется а такое, что неравенство
+ b > 0 выполняется при всех х ≠ πn , n Z .

Решение. Положим а = 0. Неравенство выполняется при b >0. Покажем теперь, что ни одно b ≤0 не удовлетворяет условиям задачи. Действительно, достаточно положить х = π /2, если а <0, и х = - π /2 при а ≥0.

Ответ. b> 0

§ 6. Показательные уравнения и неравенства

1. Уравнение h (x ) f ( x ) = h (x ) g ( x ) при h (x ) > 0 равносильно совокупности двух систем
и

2. В частном случае (h (x )= a ) уравнение а f (x ) = а g (x ) при а > 0, равносильно совокупности двух систем

и

3. Уравнение а f (x ) = b , где а > 0, a ≠1, b >0, равносильно уравнению

f (x )= log a b . Случай а =1 рассматриваем отдельно.

Решение простейших показательных неравенств основано на свойстве степени. Неравенство вида f (a x ) > 0 при помощи замены переменной t = a x сводится к решению системы неравенств
а затем к решению соответствующих простейших показательных неравенств.

При решении нестрого неравенства необходимо к множеству решений строгого неравенства присоединить корни соответствующего уравнения. Как и при решении уравнений во всех примерах, содержащих выражение а f (x ) , предполагаем а > 0. Случай а = 1 рассматриваем отдельно.

Пример 1 . При каких а уравнение 8 х =
имеет только положительные корни?

Решение. По свойству показательной функции с основанием, большим единицы, имеем х>0
8 х >1

>1

>0, откуда a (1,5;4).

Ответ. a (1,5;4).

Пример 2. Решить неравенство a 2 ∙2 x > a

Решение . Рассмотрим три случая:

1. а< 0 . Так как левая часть неравенства положительна, а правая отрицательна, то неравенство выполняется для любых хR .

2. a =0. Решений нет.

3. а > 0 . a 2 ∙2 x > a
2 x >
x > - log 2 a

Ответ. хR при а > 0; решений нет при a =0; х (- log 2 a ; +) при а> 0 .

§ 7. Логарифмические уравнения и неравенства

Приведем некоторые эквивалентности, используемые при решении логарифмических уравнений и неравенств.

1. Уравнение log f (x ) g (x ) = log f (x ) h (x ) равносильно системе

В частности, если а >0, а ≠1, то

log a g (x)= log a h(x)

2. Уравнение log a g (x)=b
g (x)= a b ( а >0, a ≠ 1, g(x) >0).

3. Неравенство log f ( x ) g (x ) ≤ log f ( x ) h (x ) равносильно совокупности двух систем:
и

Если а, b – числа, а >0, а ≠1, то

log a f (x) ≤ b

log a f (x) > b

Пример 1. Решите уравнение

Решение . Найдем ОДЗ: х > 0, х ≠ а 4 , a > 0, а ≠ 1. Преобразуем уравнение

logх – 2 = 4 – log a x
logх + log a x – 6 = 0, откуда log a x = - 3

х = а -3 и log a x = 2
х = а 2 . Условие х = а 4
а – 3 = а 4 или а 2 = а 4 не выполняется на ОДЗ.

Ответ: х = а -3 , х = а 2 при а (0; 1)
(1; ).

Пример 2 . Найдите наибольшее значение а , при котором уравнение

2 log -
+ a = 0 имеет решения.

Решение. Выполним замену
= t и получим квадратное уравнение 2 t 2 – t + a = 0. Решая, найдем D = 1-8 a . Рассмотрим D ≥0, 1-8 а ≥0
а ≤.

При а = квадратное уравнение имеет корень t = >0.

Ответ. а =

Пример 3 . Решить неравенство log (x 2 – 2 x + a ) > - 3

Решение. Решим систему неравенств

Корни квадратных трехчленов х 1,2 = 1 ±
и х 3,4 = 1 ±
.

Критические значения параметра: а = 1 и а = 9.

Пусть Х 1 и Х 2 – множества решений первого и второго неравенств, тогда

Х 1
Х 2 = Х – решение исходного неравенства.

При 0< a <1 Х 1 = (- ;1 -
)
(1 +
; +), при а > 1 Х 1 = (-;+).

При 0 < a < 9 Х 2 = (1 -
; 1 +
), при а ≥9 Х 2 – решений нет.

Рассмотрим три случая:

1. 0< a ≤1 Х = (1 -
;1 -
)
(1 +
;1 +
).

2. 1 < a < 9 Х = (1 -
;1 +
).

3. a ≥ 9 Х – решений нет.

Задачи ЕГЭ

Высокий уровень С1, С2

Пример 1. Найдите все значения р , при которых уравнение

р ∙ ctg 2 x + 2sinx + p = 3 имеет хотя бы один корень.

Решение. Преобразуем уравнение

р ∙ (
- 1) + 2sinx + p = 3, sinx =t , t
, t 0.

- p + 2 t + p = 3, + 2 t = 3, 3 -2t = , 3t 2 – 2t 3 = p .

Пусть f (y ) = 3 t 2 – 2 t 3 . Найдем множество значений функции f (x ) на


. у / = 6 t – 6 t 2 , 6 t - 6 t 2 = 0, t 1 =0, t 2 = 1. f (-1) = 5, f (1) = 1.

При t
, E (f ) =
,

При t
, E (f ) =
, то есть при t


, E (f ) =
.

Чтобы уравнение 3 t 2 – 2 t 3 = p (следовательно, и данное) имело хотя бы один корень необходимо и достаточно p E (f ), то есть p
.

Ответ.
.

Пример 2.

При каких значениях параметра а уравнение log
(4 x 2 – 4 a + a 2 +7) = 2 имеет ровно один корень?

Решение. Преобразуем уравнение в равносильное данному:

4x 2 – 4a + a 2 +7 = (х 2 + 2) 2 .

Отметим, что если некоторое число х является корнем полученного уравнения, то число – х также является корнем этого уравнения. По условию это не выполнимо, поэтому единственным корнем является число 0.

Найдем а .

4∙ 0 2 - 4a + a 2 +7 = (0 2 + 2) 2 ,

a 2 - 4a +7 = 4, a 2 - 4a +3 = 0, a 1 = 1, a 2 = 3.

Проверка.

1) a 1 = 1. Тогда уравнение имеет вид: log
(4 x 2 +4) =2. Решаем его

4x 2 + 4 = (х 2 + 2) 2 , 4x 2 + 4 = х 4 + 4x 2 + 4, х 4 = 0, х = 0 – единственный корень.

2) a 2 = 3. Уравнение имеет вид: log
(4 x 2 +4) =2
х = 0 – единственный корень.

Ответ. 1; 3

Высокий уровень С4, С5

Пример 3. Найдите все значения р, при которых уравнение

х 2 – (р + 3)х + 1= 0 имеет целые корни и эти корни являются решениями неравенства: х 3 – 7р х 2 + 2х 2 – 14 р х - 3х +21 р ≤ 0.

Решение. Пусть х 1, х 2 – целые корни уравнения х 2 – (р + 3)х + 1= 0. Тогда по формуле Виета справедливы равенства х 1 + х 2 = р + 3, х 1 ∙ х 2 = 1. Произведение двух целых чисел х 1 , х 2 может равняться единице только в двух случаях: х 1 = х 2 = 1 или х 1 = х 2 = - 1. Если х 1 = х 2 = 1, то р + 3 = 1+1 = 2
р = - 1; если х 1 = х 2 = - 1, то р + 3 = - 1 – 1 = - 2
р = - 5. Проверим являются ли корни уравнения х 2 – (р + 3)х + 1= 0 в описанных случаях решениями данного неравенства. Для случая р = - 1, х 1 = х 2 = 1 имеем

1 3 – 7 ∙ (- 1) ∙ 1 2 +2∙ 1 2 – 14 ∙ (- 1) ∙ 1 – 3 ∙ 1 + 21 ∙ (- 1) = 0 ≤ 0 – верно; для случая р = - 5, х 1 = х 2 = - 1 имеем (- 1) 3 – 7 ∙ (- 5) ∙ (-1) 2 + 2 ∙ (-1) 2 – 14 ∙ (-5) × (- 1) – 3 ∙ (- 1) + 21∙ (-5) = - 136 ≤ 0 – верно. Итак, условию задачи удовлетворяют только р = - 1 и р = - 5.

Ответ. р 1 = - 1 и р 2 = - 5.

Пример 4. Найдите все положительные значения параметра а , при которых число 1 принадлежит области определения функции

у = (а
- а
).